Кинематика сплошной среды. Способы изучения движения деформируемых сред. Перемещение деформируемого тела, страница 7

Отсюда следует, что произошло вращение элемента в координатной плоскости  вокруг координатной оси .

2.5.3.Тензор деформаций Альманси-Гамелия

В механике жидкости и газа, а иногда и в механике твердого деформируемого тела используется эйлерова система координат. В эйлеровой системе координат  координаты произвольной точки М в начальный момент времени t₀ выражаются через пространственные координаты соотношением (2.3). Из этого соотношения следует, что дифференциал

где введено обозначение

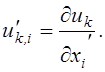
Тензор деформации Альманси –Гамеля вводится через квадрат расстояния между двумя произвольными бесконечно близкими точками M и N (рис.11) до деформации:

Здесь через  обозначен тензор деформаций Альманси- Гамеля:

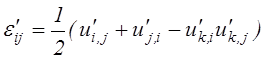
Тензор деформаций Альманси-Гамеля является симметричным тензором второго ранга пространственной (эйлеровой) системы координат.

Через тензор деформаций Альманси-Гамеля можно выразить линейные и сдвинутые деформации. Вывод соответствующих выражений предоставляется в качестве упражнения.

2.6. Главные компоненты тензора деформаций и главные

оси деформации

2.6.1. Главные компоненты тензора деформаций

Из формулы (2.12) следует, что величина относительной линейной деформации в произвольной точке M по любому направлению MN зависит от ориентации элемента MN в пространстве, т.е. от направляющих косинусов . Таким образом,  величину  можно рассматривать как функцию независимых переменных . Изменяя величины направляющих косинусов непрерывно с возвратом в исходное положение, получим в соответствии с формулой (2.12) непрерывное изменение деформации , которая в исходном положении совпадает с первоначальным значением. Из курса математического анализа известно, что если непрерывная функция при изменении аргумента принимает несколько одинаковых значений, то она может иметь экстремальные точки.

Для определения экстремальных значений деформации элемента MN воспользуемся методом неопределённых множителей Лагранжа. Неопределенный множитель Лагранжа введем с помощью известной формулы , где направляющие косинусы  определяются равенством (2.11). Эта формула легко находится из равенства , см. п. 2.2. Она позволяет переписать формулу (2.12) в виде

где – множитель Лагранжа, определяющий некоторую деформацию. Величина , поэтому приведённое выражение полностью эквивалентно (2.12). Экстремальные значения функции F  находятся из условия 

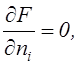
которое позволяет получить следующую однородную систему уравнений

                                                (2.26)

Так как   то направляющие косинусы не могут быть одновременно равными нулю. Поэтому нетривиальное решение однородной системы уравнений (2.26) возможно лишь в случае, когда её определитель равен нулю:

В развёрнутом виде полученный определитель записывается следующим образом:

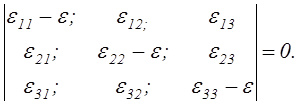
Раскрывая этот определитель, получим кубическое уравнение относительно множителя Лагранжа:

                                        (2.27)

где

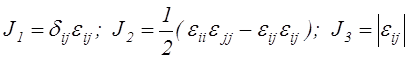                          (2.28)

или в развёрнутом виде

          (2.28')

Из теории решения кубических уравнений известно, что кубическое уравнение имеет хотя бы один вещественный корень. Обозначим вещественный корень кубического уравнения (2.27) через . Так как формула (2.12) записана в произвольной декартовой системе координат, то можно рассмотреть задачу определения экстремальных значений деформации в лагранжевой системе координат, которая в начальный момент времени будет повёрнута относительно пространственной системы координат таким образом, чтобы направление линейного элемента, получившего экстремальную деформацию , совпало бы с осью х₁. Тогда в общем случае при , , так как направляющие косинусы рассматриваются относительно осей пространственной системы координат. Для такой системы координат первое уравнение (2.26) запишется в виде:

                                    (2.29)