При выводе всех соотношений настоящей главы предполагалось однозначность и непрерывность перемещений и всех их частных производных до третьего порядка включительно. Тем самым применимость полученных уравнений и соотношений ограничена однородными телами с непрерывной неоднородностью, удовлетворяющей принятым предположениям. Для неоднородных тел, изготовленных из различных материалов, частные производные от функций перемещений могут иметь разрывы первого рода, которые образуют границы, разделяющие тело на отдельные области. В пределах каждой области имеет место полное удовлетворение принятых предположений. Поэтому полученные уравнения и соотношения полностью применимы для описания деформированного состояния внутренних частей каждой такой области. На границах этих областей должны выполнятся условия неразрывности перемещений, поскольку в противном случае нарушается целостность тела. Условие неразрывности перемещений могут быть записаны в виде:
![]() ,
(2.69) где индексами
,
(2.69) где индексами ![]() и
и ![]() обозначены две
соприкасающиеся области тела.
обозначены две
соприкасающиеся области тела.
В теории пластичности и ползучести широкое применение находят приращения деформаций и скорости их изменения, которые приобретают бесконечно малые объёмы сплошного тела за бесконечно малый промежуток времени dt в любой фиксированный момент времени t. Скорость изменения перемещений сплошного тела в любой его точке при использовании лагранжевых координат равна:
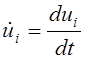 ,
(2.70)
,
(2.70)
где ![]() представляют
собой приращения перемещений за бесконечно малый промежуток времени,
представляют
собой приращения перемещений за бесконечно малый промежуток времени, ![]() . Очевидно, что приращения
перемещений и их частные производные
. Очевидно, что приращения
перемещений и их частные производные ![]() являются
бесконечно малыми величинами, так как величины
являются
бесконечно малыми величинами, так как величины ![]() и
и
![]() конечны, а dt
– бесконечно мала.
конечны, а dt
– бесконечно мала.
За приращение компонентов тензора
деформаций ![]() принимается их изменения,
связанные с бесконечно малыми деформациями, которые приобретает сплошное тело
за бесконечно малый промежуток времени. Подставляя в уравнение (2.9) вместо
производных перемещений производные от их приращений, получим
принимается их изменения,
связанные с бесконечно малыми деформациями, которые приобретает сплошное тело
за бесконечно малый промежуток времени. Подставляя в уравнение (2.9) вместо
производных перемещений производные от их приращений, получим
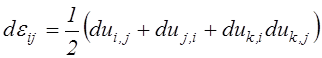 . (2.71)
. (2.71)
Обратим внимание на то, что
приращение компонентов деформаций ![]() не
являются дифференциалами
не
являются дифференциалами ![]() , и не
могут быть получены формальным дифференцированием уравнения (2.9). Нелинейные
слагаемые в (2.71) являются бесконечно малыми величинами высшего порядка
малости, вследствие чего приращения компонентов деформации приводятся к форме:
, и не
могут быть получены формальным дифференцированием уравнения (2.9). Нелинейные
слагаемые в (2.71) являются бесконечно малыми величинами высшего порядка
малости, вследствие чего приращения компонентов деформации приводятся к форме:
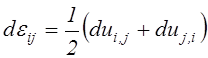 . (2.72)
. (2.72)
На основании определения скорости перемещений (2.70) равенство (2.72) может быть записано в виде:
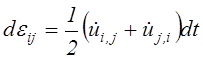 (2.73)
(2.73)
По аналогии с интенсивностью деформаций (2.49) вводится понятие интенсивности приращений деформаций
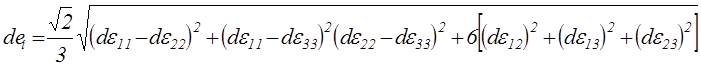 (2.74)
(2.74)
и интенсивность приращения пластических деформаций
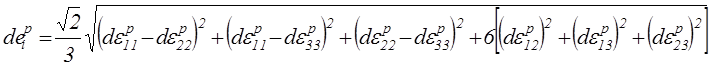 ,
(2.75) где
,
(2.75) где ![]() компоненты
тензора приращений пластических деформаций. В сокращенной форме, с
использованием тензорной символики, интенсивности приращений деформации (2.74)
и (2.75) записываются в виде:
компоненты
тензора приращений пластических деформаций. В сокращенной форме, с
использованием тензорной символики, интенсивности приращений деформации (2.74)
и (2.75) записываются в виде:
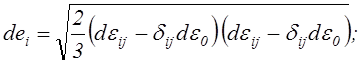
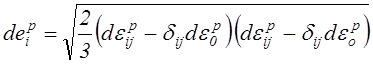 ,
(2.76) где
,
(2.76) где 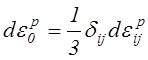 .
Точно так же вводится интенсивность приращения деформаций ползучести
.
Точно так же вводится интенсивность приращения деформаций ползучести ![]() .
.
Определив скорости изменения компонентов тензора деформаций равенством
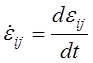 ,
(2.77)
,
(2.77)
где ![]() –
приращение компонентов тензора деформаций (2.72), выразим их с помощью (2.73)
через скорости изменения перемещений
–
приращение компонентов тензора деформаций (2.72), выразим их с помощью (2.73)
через скорости изменения перемещений
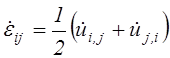 .
(2.78)
.
(2.78)
Формула (2.78) определяет тензор скорости деформаций.
По аналогии с интенсивностями деформаций и приращений деформаций можно определить интенсивность скоростей деформаций
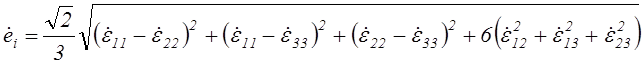 (2.79)
(2.79)
или в сокращенной форме, с использованием тензорной символики
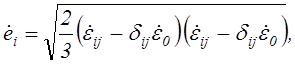 (2.80)
(2.80)
где
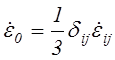 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.