Кинематика сплошной среды. Способы изучения движения деформируемых сред. Перемещение деформируемого тела, страница 2

Рассмотрим произвольное сплошное тело, которое может быть твердым,  жидким или газообразным. Пусть это тело в некоторый момент времени t = t₀ занимает в евклидовом  пространстве объём V Положение каждой точки этого тела в начальный момент времени t = t₀ определим их проекциями на оси пространственной прямоугольной декартовой системы координат x_i (i = 1, 2, 3,), x_i   V. Предположим, что в результате внешних воздействий (загрузка, нагревание и т.д.), рассматриваемое тело в некоторый момент времени t = t₀ займёт в евклидовом пространстве объём . Тогда все точки этого тела изменят своё положение в пространстве, т.е. получат какие – то перемещения, проекции которых в выбранной системе координат равны  u_i, а  положение любой произвольной точки М определяется проекция   

                                             (2.1)

см. рис. 10.     

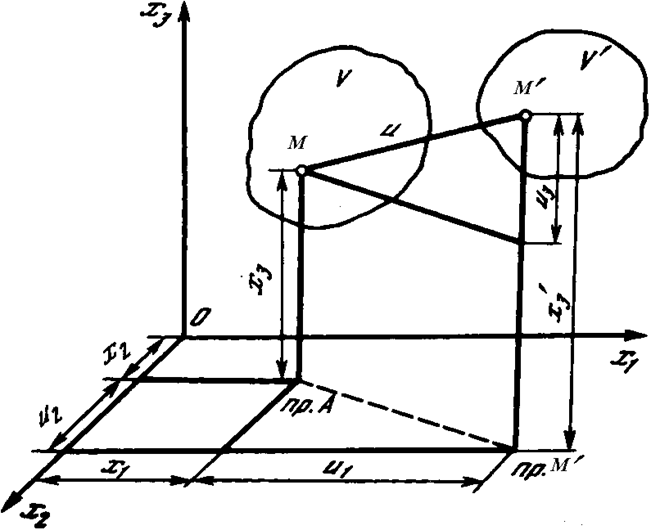Рис. 10. Определение проекции перемещения точки М при внешних воздействиях на тело.

Проекции перемещения, которые будем называть компонентами  перемещения или просто перемещениями, являются функциями координат рассматриваемой точки и времени t, u_i = u_i (х₁, х₂, х_3, t). Их будем считать однозначными и непрерывными вместе со всеми частными производным по координатам включительно до третьего  порядка. Вследствие этого формула (2.1) для каждого момента времени устанавливает взаимно однозначное соответствие между координатами  и , так как на основании концепции сплошности деформируемого тела каждой его точке до деформации соответствует только одна точка после деформации. По этой причине формулу (2.1) можно рассматривать как некоторое преобразование координат, причём параметры x_i, введенные как декартовые координаты точек деформируемого тела до деформации, можно использовать как криволинейные координаты для описания положения точек этого тела после деформации. Тем самым можно перейти от описания перемещений деформируемого тела в пространственной системе координат к их описанию в материальной системе.

2.1.3. Способы описания движения сплошных тел

Как мы уже знаем, вследствие изменений размеров и формы тела при деформации, все точки тела, лежащие до деформации на прямых, параллельных соответствующим осям исходной системы координат, в деформируемом теле образуют в общем случае кривые линии. Положение сдеформированных координатных линий определяется формулой (2.1) путём фиксации соответствующих координат в начальный момент времени t₀. Например, при х₂ = х₂⁰, х₃ = х₃⁰ формула (2.1) приводится к трём уравнениям, определяющим кривую, на которой лежат точки, принадлежащие до деформации прямой, параллельной оси Х₁:

                                   (2.2)

Замечательным свойством рассмотренной системы криволинейных координат является то, что в ней положение произвольной точки деформируемого тела в любой момент времени численно определяется теме же координатами, что и в исходном недеформированном состоянии. Поэтому уравнение любой линии, записанное в координатах  x_i в недеформированном теле, полностью сохраняет свой вид в деформированном теле, а поле перемещений u_i в любой момент времени t выражается через положения точек в недеформированном состоянии тела в момент t = t₀ . Представленное описание поля принято связывать с именем Лагранжа, а координаты x_i носят название лагранжевых или материальных координат, хотя фактически эти координаты были введены в 1761 г. Эйлером [9]. Лагранжевы координаты x_i и время t носят название лагранжевых переменных.

Наряду с описанием Лагранжа применяется другой способ, который связывают с именем Эйлера. Фактически этот способ предложен Даламбером в 1752 г. [9]. В способе Эйлера в качестве независимых координат принимаются координаты пространственной системы , относящиеся к положению материальной точки в момент времени t. Координаты носят название эйлеровых или пространственных координат. Эйлеровы координаты совместно с временем t называются эйлеровыми переменными. В способе Эйлера перемещения u_i рассматриваются, как функции  и t. В этом способе вместо (2.1) будем иметь