Кинематика сплошной среды. Способы изучения движения деформируемых сред. Перемещение деформируемого тела, страница 9

В связи с тем, что решением уравнения (2.27) являются главные компоненты тензора деформаций, которые были обозначены через  то уравнение (2.27) можно представить в следующем эквивалентном виде

или

Последнее уравнение позволяет выразить инварианты тензора деформаций через главные компоненты тензора деформаций:

              (2.32)  

Таким образом, инварианты тензора деформаций могут быть выражены через компоненты тензора деформаций в произвольной системе декартовых  координат по формулам (2.28) и через главные компоненты тензора деформаций по формулам (2.32).

2.8. Объёмная деформация и деформация координатных площадок

2.8.1. Объёмная деформация

Рассмотрим объёмную деформацию элементарного параллелепипеда с рёбрами, направления которых после деформации совпадут с главными осями деформации. На основании результатов, полученных в п.2.6, можно утверждать, что рёбра такого параллелепипеда будут взаимно перпендикулярными как до деформации, так и после деформации. Пусть размеры рёбер до деформации тела равны . Тогда объём элементарного параллелепипеда до деформации оказывается равным    Размеры  рёбер параллелепипеда после деформации обозначим через  Объём элементарного параллелепипеда после деформации равен 

Поскольку направления рёбер параллелепипеда после деформации совпадают с главными осями деформации, то относительные линейные деформации этих рёбер равны главным деформациям  Последние по определению находятся из следующего равенства 

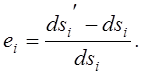
Отсюда   

и          

Относительная объёмная деформация, задаваемая выражением

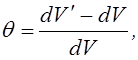
оказывается равной

                                  (2.33) 

В формулу (2.33)  входят главные деформации  той точки, в окрестностях которой определяется относительная объёмная деформация.

С помощью формул (2.31) и (2.32) относительная объёмная деформация  выражается через инварианты тензора деформаций

                                  (2.34)     

Отсюда следует что, относительная объёмная деформация является инвариантом. Собственно, этого и следовало ожидать, так как деформация тела не зависит от выбранной системы координат.

Если воспользоваться значениями инвариантов тензора деформаций (2.28), то относительную объёмную деформацию можно выразить через компоненты тензора деформаций  Вывод формулы (2.34) и выражение относительной объёмной деформации через компоненты  предоставляется в качестве самостоятельного упражнения.

2.8.2. Деформация координатных площадок

Рассмотрим деформацию элементарной координатной площадки  с направляющим косинусом  В результате деформации сплошного тела элемент  превратится с точностью до величины высшего порядка малости в косоугольный параллелограмм, площадь которого равна:

Из определения деформации следует, что

а с помощью формулы (2.22) находим, что

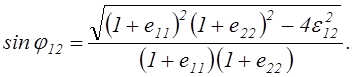
В результате площадь деформированной площадки  оказывается равной

                           (2.35)

Относительное изменение площади координатной площадки, произошедшее вследствие её деформации, после подстановки величин компонентов деформации (2.13) и (2.14) примет вид:

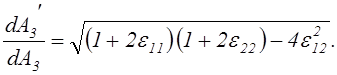                                (2.36)

Аналогично находятся относительные изменения площадей оставшихся двух координатных площадок:

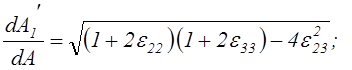
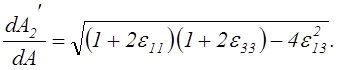                            (2.36’)

2.9. Случай малых деформаций

2.9.1. Общие соотношения

Наибольший практический интерес представляет случай, когда относительные линейные деформации и углы сдвига пренебрежимо малы по сравнению с единицей. Лишь при этом условии возможна нормальная эксплуатация практически всех инженерных сооружений и конструктивных элементов. Исключения представляют только некоторые изделия из резины и полимерных материалов.

Полагая, что  из формулы (2.12) получим

                                                   (2.37)

Размещая элемент MN параллельно координатной оси , получим лишь один направляющий косинус, отличный от нуля. В результате формула (2.37) позволяет установить следующие равенства: