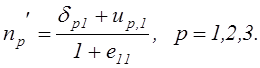Кинематика сплошной среды. Способы изучения движения деформируемых сред. Перемещение деформируемого тела, страница 5

                                          (2.16)

Здесь                 

Аналогичные формулы могут быть получены и для двух других отрезков, которые до деформации совпадали с направлениями координатных осей х₂ и х₃:  

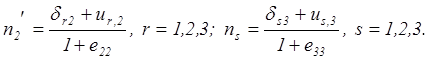                (2.16')                      

2.3.2. Формула преобразования локального базиса

Равенства (2.16), (2.16') позволяют получить формулу преобразования локального базиса деформированной лагранжевой системы координат через локальный базис недеформированных координат. Под локальным базисом будем понимать единичные вектора, которые в каждой точке тела направлены по касательным к координатным линиям в сторону их возрастания. Локальный базис недеформированной системы лагранжевых координат, единичные вектора которого  обозначим через , совпадает  с направлениями декартовых координат принятой системы отсчёта, т.е. направления единичных векторов  совпадают с направлениями пространственных координат  . Направления единичных векторов   локального базиса деформированной лагранжевой системы координат совпадают с направлениями касательных к координатным линиям в момент времени t>t₀.

Для введённых таким образом локальных базисов имеем очевидное равенство   которое позволяет представить формулу (2.16) в виде

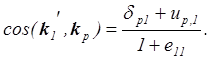
Полученное равенство помогает установить разложение вектора  по направлениям  

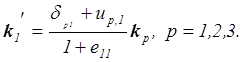                                       (2.17)

Обобщив формулу (2.17) на два других единичных вектора  и  получим искомую формулу преобразования локального базиса лагранжевой системы координат при её деформации, выразив единичные вектора локального базиса, после деформации, через единичные вектора до деформации,

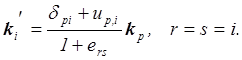                                       (2.18)

2.4. Деформация сдвига

Исследуем изменение углов в некоторой точке М по произвольным направлениям при деформации сплошного тела. С этой целью зададим в точке М недеформированного тела произвольный угол двумя любыми направлениями с помощью бесконечно близких точек N₁ и N₂. Направляющие косинусы отрезка MN₁ обозначены через  , а отрезка MN₂ – через  . Направляющие косинусы этих же отрезков после деформации обозначим так: элемента  через , а элемента - через . Угол  между отрезками MN₁ и MN₂ до деформации обозначим через , а после деформации – через . Косинусы этих углов определяются известными из курса дифференциальной геометрии формулами:

                                    (2.19)

Направляющие косинусы обоих рассматриваемых направлений I и II в деформированном состоянии можно с помощью формулы (2.15) выразить через направляющие косинусы до деформации:

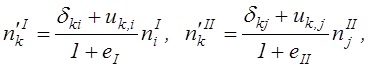
где через  и  обозначены относительные линейные деформации отрезков MN₁ и MN₂. Подставив полученные выражения во вторую формулу (2.19), найдём, что

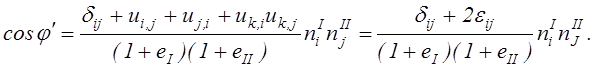
Привлекая первую формулу (2.19), получим

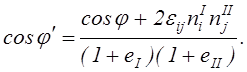
Приняв угол 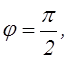 а 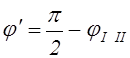, приведём полученное выражение к виду:

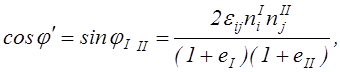                                  (2.20)

Здесь угол  представляет собой деформацию сдвига в плоскости N₁MN₂.

Если элемент MN₁ совпадает с координатной линией х₁, а элемент MN₂ – с координатной линией х₂, то , тогда как остальные направляющие косинусы обоих элементов оказываются равными нулю. В результате формула (2.20) приведётся к виду:

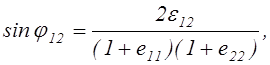                                          (2.21)

где  представляет собой деформацию сдвига в точке М в координатной плоскости Ох₁х₂. Аналогично выводится формула, определяющая деформацию сдвига в произвольной точке М в любой координатной плоскости:

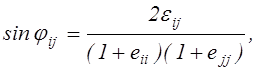
                                         (2.21)

Углы   определяют деформацию сдвига в координатных плоскостях ,  для любой произвольной точки М.

2.5. Тензоры деформаций и вращений

2.5.1 Тензор деформаций Грина