Поскольку ![]() является
решением первого уравнения (2.26), то последнее равенство тождественно равно
нулю при любых направляющих косинусах
является
решением первого уравнения (2.26), то последнее равенство тождественно равно
нулю при любых направляющих косинусах ![]() Последнее
возможно только при условии
Последнее
возможно только при условии ![]() Тем
самым попутно получено доказательство отсутствия деформаций сдвига, см. (2.21') между линейным элементом,
получающим экстремальную деформацию, и любым другим перпендикулярным к нему
элементом.
Тем
самым попутно получено доказательство отсутствия деформаций сдвига, см. (2.21') между линейным элементом,
получающим экстремальную деформацию, и любым другим перпендикулярным к нему
элементом.
На основании (2.29) в рассматриваемой системе координат определитель системы однородных уравнений (2.26) запишется в виде
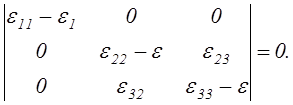
Раскрывая этот определитель получим уравнение
![]() (2.30) или
(2.30) или
![]() (2.30')
(2.30')
Уравнение (2.30) вещественны. Следовательно, в каждой точке тела всегда можно указать три направления, в которых относительные линейные деформации принимают экстремальные значения. Эти деформации носят название главных деформаций, а корни уравнения (2.27) называются главными компонентами тензора деформаций. Главные деформации и главные компоненты тензора деформаций обозначаются соответственно:
![]()
Направления, соответствующие главным
деформациям носят название главных осей деформации. Направляющие косинусы,
определяющие направления главных осей деформации,![]() ,
находятся из уравнения (2.26) путём подстановки в него поочерёдно главных
компонентов тензора деформаций.
,
находятся из уравнения (2.26) путём подстановки в него поочерёдно главных
компонентов тензора деформаций.
Покажем, что главные оси деформации
ортогональны друг к другу. Если ![]() определяет
направление
определяет
направление ![]() , а
, а ![]() - направление
- направление ![]() , то из уравнения (2.26) имеем:
, то из уравнения (2.26) имеем:
![]()
Умножим первое равенство на ![]() , а второе на
, а второе на ![]() и просуммируем их по
и просуммируем их по ![]() :
:
![]()
Нетрудно убедиться в равенстве между
собой левых частей последних равенств. Поменяв немые индексы суммирования левой
части первого равенства местами, получим ![]() а
так как
а
так как ![]() то
то ![]() Поэтому при вычитании
второго равенства из первого получим
Поэтому при вычитании
второго равенства из первого получим
![]()
Так как в общем случае ![]() то
то ![]() откуда и следует ортогональность
главных осей деформации
откуда и следует ортогональность
главных осей деформации ![]() и
и ![]() , см. (2.19). Аналогично
доказывается ортогональность всех главных осей деформации.
, см. (2.19). Аналогично
доказывается ортогональность всех главных осей деформации.
Несколько выше было доказано отсутствие деформаций сдвига между линейным элементом, получающим экстремальную деформацию, и любым другим элементом перпендикулярным к первому. Отсюда следует, что в каждой точке тела до деформации могут быть указаны три таких взаимно перпендикулярных направления, которые и после деформации остаются взаимно перпендикулярными. После деформации эти направления совпадают с главными осями деформации.
Значение главных компонентов тензора
деформаций ![]() находятся путём решения
кубического уравнения (2.27). После чего легко определяются главные деформации.
Совместив координатные оси с главными осями, по формуле (2.12) найдём значения
главных деформаций
находятся путём решения
кубического уравнения (2.27). После чего легко определяются главные деформации.
Совместив координатные оси с главными осями, по формуле (2.12) найдём значения
главных деформаций
![]() (2.31)
(2.31)
В зависимости от числа главных компонентов тензора деформаций, отличных от нуля, различают три вида деформированного состояния в точке:
одноосное или линейное, когда отличаются от нуля одна главная компонента
![]()
плоское, когда две главных компоненты отличны от нуля
![]()
пространственное или объёмное, когда ни одна из главных компонент не равна нулю
![]()
![]()
В общем случае в различных точках одного и того же сплошного тела могут быть все три вида деформированного состояния – в каждой точке своё.
Вернёмся к уравнению (2.27),
определяющему главные компоненты тензора деформаций. Поскольку деформация
сплошного тела не зависит от принятой системы координат, то независимыми от
координатной системы будут и главные компоненты тензора деформаций. Но
последнее возможно только в том случае, когда коэффициенты уравнения (2.27) ![]() также не зависят от выбора
координатной системы. Эти коэффициенты, определяемые выражениями (2.28), носят
названия инвариантов тензора деформаций, соответственно первым, вторым и
третьим инвариантам.
также не зависят от выбора
координатной системы. Эти коэффициенты, определяемые выражениями (2.28), носят
названия инвариантов тензора деформаций, соответственно первым, вторым и
третьим инвариантам.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.