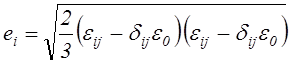Кинематика сплошной среды. Способы изучения движения деформируемых сред. Перемещение деформируемого тела, страница 11

                                      (2.47)

и  интенсивности деформаций сдвига

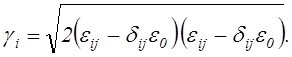                                    (2.48)

В развёрнутом виде интенсивности деформаций  и интенсивности деформаций сдвига  записываются следующем образом:

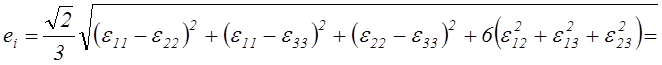
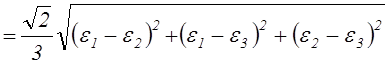                              (2.49)

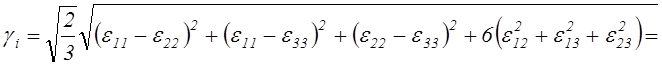
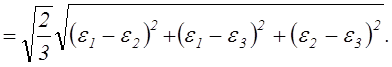                               (2.50)

В случае линейного деформированного состояния имеем: ; ; Подстановка этих значений в (2.49) позволяет представить величину интенсивности деформаций при линейном деформированном состоянии в виде  В случае чистого сдвига    и по формуле (2.50) находим, что  Таким образом введение странных на первый взгляд коэффициентов в формулы интенсивностей деформаций (2.49) и (2.50) объясняется тем, что в случаях линейного деформированного состояния и чистого сдвига эти формулы определяют соответственно девиатор тензора деформации и деформацию сдвига.

Аналогично формуле (2.47) интенсивности пластических деформаций и деформаций ползучести  определяются выражениями:

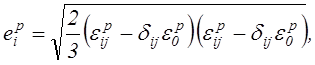                                         (2.51)

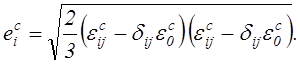                                          (2.52)      

Развернутые выражения (2.51) и (2.52) аналогичны формуле (2.49).

В теории пластичности находит применение также величина

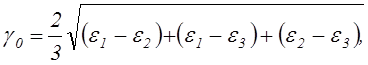                                  (2.53)

которая называется октаэдрической угловой деформацией и представляет собой наибольшую деформацию сдвига между октаэдрической площадкой, т.е. площадкой, равнонаклонённой к координатным осям, и перпендикулярным к этой площадке направлением.

Интенсивности деформаций и октаэдрическая угловая деформация являются производными инвариантами второго инварианта девиатора тензора деформаций и определяют искажение формы элементарных объёмов деформируемого тела, не затрагивая их величины.

2.10. Случаи малых деформаций и малых приращений

перемещений

Рассмотрим случаи, когда по сравнению с единицей малы не только деформации, но и приращения перемещений в направлении координат. Известно, что частные производные какой – либо функции по  с геометрической точки зрения представляют собой тангенсы углов наклона касательных к координатным линиям . Тем самым они характеризуют приращения функции в направлениях . Поэтому, говоря о малых приращениях перемещений в направление координатной линии , мы подразумеваем малость по сравнению с единицей производных . Считая, что приращения перемещений  малы по сравнению с единицей, отметим три случая: 1) все приращения перемещений являются величинами одного порядка малости; 2) приращение перемещений  являются величинами более низкого порядка малости по сравнению с остальными приращениями приращений; 3) приращения перемещений  и  могут иметь одинаковый порядок малости, который ниже порядка малости остальных величин приращений перемещений. Все три случая записаны для тел, ориентированных в декартовой системе координат таким образом, что наибольший размер направлен в сторону координатной оси , а наименьший – в сторону оси .

Для тел, у который все три измерения не имеют существенных отличий, применим первый случай. Для оболочечных тел применимы первый и второй случай: при малых прогибах (перемещениях ) применим первый случай, при больших - второй. Для стержневых тел возможно применение трёх случаев: при малых величинах поперечных перемещений применим первый случай; при малом перемещении в направлении – второй; при больших перемещениях в направлениях  и  – третий случай. Здесь учитываются лишь относительные перемещения точек тела. Перемещения тела, как жесткого целого, из рассмотрения исключаются.

Для первого случая все произведения  являются величинами высшего порядка малости в сравнении с производными . Поэтому без ущерба для точности определения компонентов тензора деформаций ими можно пренебречь. В результате равенства (2.9) приводятся к виду

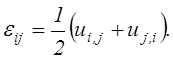                                                 (2.54)