![]() (2.3)
(2.3)
Отсюда следует, что точки сплошного
тела, лежащие в момент времени t>t0 на прямых, которые параллельны координатным линиям пространственной
системы координат, в недеформированном теле будут принадлежать кривым линиям.
Для определения последних достаточно в момент времени t зафиксировать две любые координаты и решить систему уравнений (2.3)
при t = t0. Например, примем![]() Тогда три уравнения,
определяющие в пространственной системе координат кривую линию, на которой до
деформации располагались точки тела, находящиеся в момент времени t на прямой, параллельной координатной оси Х1:
Тогда три уравнения,
определяющие в пространственной системе координат кривую линию, на которой до
деформации располагались точки тела, находящиеся в момент времени t на прямой, параллельной координатной оси Х1:
![]()
![]() (2.4)
(2.4)
![]()
Отсюда следует, что координаты линии ![]() определяют в теле до деформации
те кривые, которые в момент времени t образуют прямые,
параллельные осям декартовой системы координат Хi.В
разные моменты времени прямые, параллельные координатным осям, содержат
различные точки тела. Эйлеровы координаты определяют точки пространства. В этом
их коренное отличие от лагранжевых координат xi, которые определяют конкретные точки деформируемого тела.
определяют в теле до деформации
те кривые, которые в момент времени t образуют прямые,
параллельные осям декартовой системы координат Хi.В
разные моменты времени прямые, параллельные координатным осям, содержат
различные точки тела. Эйлеровы координаты определяют точки пространства. В этом
их коренное отличие от лагранжевых координат xi, которые определяют конкретные точки деформируемого тела.
Оба способа описания движения сплошных тел: способ Лагранжа и способ Эйлера с математической точки зрения равноценны. Описав движение в переменных Лагранжа, можно перейти к описанию движения в переменных Эйлера или наоборот. При этом следует иметь ввиду, что любая часть деформируемого тела, которая будет заключена в правильную фигуру в одной системе координат, в другой системе координат может оказаться заключённой в неправильной фигуре. Например, элементарный тетраэдр записанный в эйлеровойт системе координат в момент времени t>t0 как правильная фигура, три грани которой параллельны координатным плоскостям, в лагранжевой системе координат в момент времени t0 исказит свою форму, углы между гранями и ориентацию в пространстве. В механике сплошных сред находят применение и способ Эйлера, и способ Лагранжа.
Способ Эйлера используется в основном
при исследовании движения жидких и газообразных сред. Это объясняется тем, что
форма и движение краевых поверхностей жидкости и газа обычно известны и
искомыми величинами являются не перемещения частиц, а их скорости. В скоростях
обычно формируются и краевые условия. Всё это позволяет не следить за
перемещениями отдельных точек среды, а интересоваться лишь распределением
скоростей в пространстве. Наиболее подходящей для этого системой координат
является эйлерова система с координатами ![]() .
.
В механике твёрдого деформируемого тела более предпочтительным является способ Лагранжа. Это объясняется тем, что краевые условия в механике деформируемого твёрдого тела задаются на краевых поверхностях, форма которых зависит от искомых величин. При использовании лагранжевых координат уравнения краевых поверхностей тела в деформируемом теле сохраняют такой же вид, как и в недеформированном состоянии. Это существенным образом упрощает постановку краевых задач механики деформируемого твёрдого тела. По этой причине дальнейшее изложение материала ведётся с использованием лагранжевых координат хi.
Исследуем в условиях деформации
сплошного тела изменение длины линейного элемента в какой – то точке М
по произвольному направлению, которое в недеформированном состоянии зададим
бесконечно близкой точкой N. Пусть точка M имеет координаты xi,
тогда бесконечно близкая к ней точка w будет иметь
координаты ![]() В результате деформации
точка М переместится в положение
В результате деформации
точка М переместится в положение ![]() с
координатами
с
координатами ![]() а точка N
в точку
а точка N
в точку ![]() с координатами
с координатами ![]()
Относительная линейная деформация в точке М по произвольному направлению MN определяется выражением
![]()
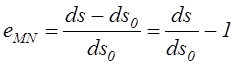 ,
(2.5)
,
(2.5)
где ![]() и
и ![]() -
расстояние между точками M и N
до и после деформации (см.§ 1.5).
-
расстояние между точками M и N
до и после деформации (см.§ 1.5).
Пользуясь тензорной символикой (см.
§1.9), запишем квадраты расстояний
между точками M и N до и после деформации
в виде: ![]()
![]() см. рис. 11.
см. рис. 11.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.