Кинематика сплошной среды. Способы изучения движения деформируемых сред. Перемещение деформируемого тела, страница 6

Из формул (2.12) и (2.21) следует, что относительные линейные деформации и деформации сдвига в любой точке тела по любым направлениям, заданным направляющими косинусами, будут полностью определены, если известны все параметры  Эти параметры формулой (2.9) связаны с перемещениями точек тела при его деформации. Непосредственно из формулы (2.9) следует, что  Таким образом, общее число независимых параметров  полностью определяющих деформированное состояние в любой точке тела, равно шести.

Из физической сущности процесса деформации тела следует, что деформированное состояние в любой точке тела не зависит от принятой системы координат. Совокупность параметров, описывающих процессы, инвариантные при любых преобразованиях системы координат, образуют математические объекты, которые носят название тензоров. При строгом математическом определение тензора вводятся определённые правила преобразования при переходе от одной системы координат к другой [13]. Эти правила выводятся из условия инвариантности математического или физического объекта в различных координатных системах. Так в декартовой системе координат условием инвариантности для тензора второго ранга являются равенства типа (2.12). Поэтому совокупность параметров  образует математический объект, который является симметричным  тензором второго ранга и называется тензором деформаций. Параметры  носят название компонентов тензора деформаций. Тензор, компоненты которого определяются формулой (2.9), был введён в механику сплошной среды Грином и называется тензором деформаций Грина. Он определяет геометрию перемещений сплошной среды. В механике сплошной среды компоненты тензора деформаций занимают место основных характеристик деформации, хотя они и обладают меньшей наглядностью, чем относительные линейные деформации и деформации сдвига. Это объясняется тем, что компоненты тензора деформаций имеют существенные математические преимущества, являясь рациональными функциями производных от перемещений и подчиняясь достаточно простому закону преобразования при переходе от одной системы координат к другой.  

Таким образом, тензор деформаций является сугубо математическим объектом, который введён в рассмотрение с целью построения наиболее простой математической модели деформированного тела.

Введём в рассмотрение линейные комбинации производных от перемещений

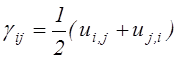                                              (2.22)            

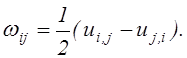                                              (2.23)

Частные производные от перемещений будут выражаться через эти параметры следующим образом

                                                   (2.24)

Через параметры  и  может быть также выражен тензор деформаций Грина (2.9):

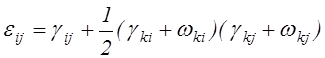                               (2.25)

Здесь суммирование по повторяющемуся индексу k производится без раскрытия скобок.

2.5.2.Тензоры деформаций и вращений Коши

Параметры  (2.22) образуют тензор бесконечно малых деформаций Коши. Пренебрегая в выражении (2.9) нелинейными слагаемыми, получим, что, при бесконечно малых деформациях  параметры имеют вполне определённый физический смысл, представляя собой линейные и угловые деформации при бесконечно малых деформациях. Для того, чтобы в этом убедиться достаточно обратиться к формулам (2.12') и (2.21'). Из формулы (2.12') находим, что при    а из формулы (2.21') получаем, что при   

Параметры  (2.23) образуют тензор вращений Коши. Они также имеют определённый физический смысл, представляя собой поворот бесконечно малого элемента тела в окрестности произвольной точки вокруг координатных осей в координатной плоскости . При этом бесконечно малый элемент рассматривается как абсолютно жёсткая недеформированная частица. Для того, чтобы убедиться в этом обратимся к формуле (2.15), определяющей изменение ориентации линейного элемента в пространстве. Полагая линейный элемент недеформируемым, получим на основании формулы (2.24), что . В случае равенства параметров  нулю имеем  и  Это означает, что при  жёсткий элемент не заменяет своей ориентации в пространстве, а значит отсутствует вращение жёсткого элемента. Теперь представим, что все параметры  за исключением одного, например , равны нулю. Тогда все производные перемещений  за исключением лишь  окажутся на основании формулы (2.24) также равными нулю. Для этого случая из формулы (2.15) находим, что