Кинематика сплошной среды. Способы изучения движения деформируемых сред. Перемещение деформируемого тела, страница 10

                                      (2.38)

Полагая малыми углы сдвига, , при малых относительных деформациях,  из формулы (2.21) получим

          .                                            (2.39)

Таким образом, при малых деформациях компоненты деформаций практически отождествляются с компонентами тензора деформаций. Последние определяются формулой (2.9).

Относительная объёмная деформация при малых деформациях находится из выражения (2.33) путём пренебрежения величинами высшего порядка малости

              (2.40)

При написании последних равенств использованы две эквивалентных формы записи первого инварианта деформации: (2.28) и (2.32).

Относительные изменения площадей элементарных площадок (2.36) при малых деформациях оказываются пренебрежимо малыми и на практике ими обычно пренебрегают. Иначе обстоит дело с направляющими косинусами. Малые деформации могут сопровождаться большими поворотами. Поэтому в некоторых задачах приходится учитывать изменение направляющих косинусов в процессе деформации. Они могут быть определены формулой (2.15) при  

                                               (2.41) 

Направляющие косинусы для направлений, которые в недеформированном состоянии были параллельны координатным осям, найдутся из формул (2.16), (2.16’) при    :

                                                  (2.42)  

2.9.2. Шаровой тензор и девиатор тензора деформаций

Деформированное состояние в любой точке тела можно разложить на две составляющие части, одна из которых определяет лишь изменение элементарного объёма, а вторая только изменение формы элементарного объёма. Первая часть называется шаровой деформацией, вторая носит название девиатора деформаций. Девиатор деформации и соответствующий ему девиатор тензора деформаций нашел широкое применение в теории пластичности.

Шаровая деформация соответствует равномерному всестороннему растяжению или сжатию при одинаковых вдоль любого направления относительных линейных деформациях . Соответствующие ей компоненты шарового тензора деформаций  равны

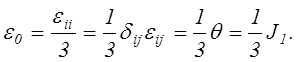                                      (2.43)

Из равенств (2.43) следует, что компоненты шарового тензора деформаций можно считать произвольным инвариантом от первого инварианта тензора деформаций. Деформации сдвига при шаровой деформации равны нулю.

Компоненты девиатора тензора деформаций равны

                                                      (2.44)

где – символ Кронекера . Из формулы (2.44) следует, что     

Таким образом, шаровой тензор деформаций определяет только изменение объёма, а девиатор тензора деформаций - только изменение формы. В общем же случае деформирования изменяются как объём, так и форма.

Произвольное разделение деформированного состояния имеет определённый физический смысл. Поскольку возникновение пластических деформаций в материале связано с образованием сдвигов, а, следовательно, с изменением формы элементарных объёмов, то критерий пластичности непосредственно выражается через девиатор тензора деформаций. При всестороннем растяжении или сжатии пластические деформации не возникают.  

2.9.3. Инварианты девиатора тензора деформаций

Инварианты девиатора тензора деформации  находятся из выражений (2.28) и (2.32), определяющих инварианты тензора деформаций, после подстановки в них значений компонентов девиатора тензора деформаций (2.44).

;  ;

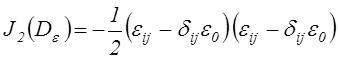.                                               (2.45)

Второй и третий инварианты девиатора тензора деформаций в развёрнутом виде имеют вид:

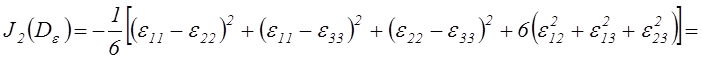
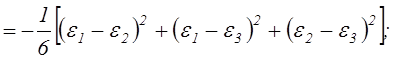
.                             (2.46)

2.9.4. Интенсивности деформаций

В уравнениях состояния нелинейной упругости, пластичности и ползучести широкое распространение получили величины, называемые интенсивностями деформаций. Интенсивности деформаций представляют собой величины, пропорциональные квадратному корню из абсолютного значения второго инварианта девиатора тензора деформаций. В зависимости от принятого коэффициента пропорциональности различают понятия интенсивности линейных деформаций или просто интенсивности деформаций