Кинематика сплошной среды. Способы изучения движения деформируемых сред. Перемещение деформируемого тела, страница 12

Соотношение (2.54) носит название уравнений Коши, а тензор с этими компонентами называется тензором деформаций Коши.

Во втором случае, когда приращения перемещений  являются величинами более низкого порядка малости по сравнению с остальными приращениями перемещений, имеем

;

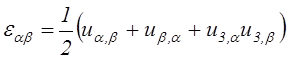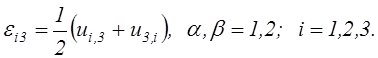
В третьем случае, когда приращения перемещений  и  могут иметь одинаковый порядок малости, который ниже порядка малости остальных величин приращений перемещений, равенства (2.9) приводятся к виду:

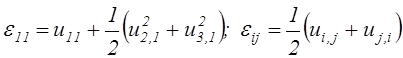,  исключая        (2.56)

В третьем случае приращение перемещений  может иметь более высокий порядок малости по сравнению с величиной . Тогда уравнения (2.56) приведутся к виду:

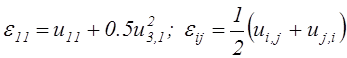, исключая            (2.57)  

Уравнениями (2.54)–(2.57) описывается геометрия сплошных сред для наиболее важных случаев деформирования конструктивных элементов инженерных сооружений и оболочечных тел искусственного и естественного происхождения.

2.11. Условия сплошности однородных и неоднородных тел

2.11.1. Уравнение сплошности однородных односвязных тел

Нетрудно видеть, что в случае, когда известны перемещения всех точек тела, то по формулам (2.9) или, при малых деформациях, по формулам (2.54)–(2.56) легко находятся все шесть компонентов тензора деформаций. Однако приходится сталкиваться и с обратной задачей.

Предположим, что в каждой точке рассматриваемого тела известны деформации. При малых деформациях это равносильно непосредственному заданию компонентов тензора деформаций, см. (2.38), (2.39). При больших деформациях компоненты тензора деформации вычисляются по формулам, приведенным в п.п. 2.2, 2.4. Таким образом, если известны деформации в каждой точке тела, то будут известны и все компоненты тензора деформаций для любой точки тела. Однако полученных соотношений явно недостаточно для однозначного определения перемещений. Действительно, для определения трёх функций перемещения в нашем распоряжении оказывается избыточное число уравнений – шесть, см., например, (2.54). Следовательно, для однозначного решения необходимо наложить на деформации какие – то ограничения. В том, что деформации не могут быть произвольными, можно убедиться также путём следующих рассуждений. Представим себе тело, рассеченное на элементарные объёмы. Легко видеть, что каждому элементарному объёму можно придать такую деформацию, что составить из них сплошное тело окажется не возможным. Ограничения, которые накладываются на деформации с целью обеспечения однозначности решения обратной задачи носят название условий сплошности тела.

Рассмотрим вывод условий сплошности тела применительно к линейным соотношениям между компонентами тензора деформаций и компонентами вектора перемещений (2.54). Для этого решим следующую задачу: найдём перемещения произвольной точки сплошного тела М, если в каждой точке этого тела известны компоненты тензора деформаций, и, кроме того, в какой-то одной точке М₀ заданы перемещения . Для того, чтобы решить поставленную задачу соединим точки М и М₀ произвольной кривой. По условию задачи в каждой точке этой кривой известны компоненты тензора деформаций . Считая приращения и их перемещения малыми, получим на основании (2.54) и (2.23) производные перемещений в виде:

Проинтегрируем это равенство по произвольной кривой М₀М

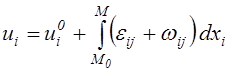.                                        (2.58)

В последнем выражении под интегралом содержится неизвестные величины – компоненты тензора вращений . Для того, чтобы их исключить из рассмотрения поступим следующим образом. Положим, что

,                                              (2.59) где – координаты точки М. Тогда второе слагаемое в криволинейном интеграле (2.58) может быть представлено в виде:

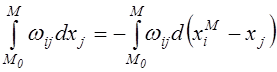
Проинтегрируем этот криволинейный интеграл по частям

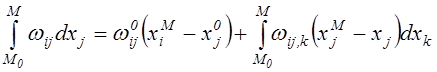.                    (2.60)