Разработка методологии теоретико-экспериментальных исследований процессов нестационарного резания на базе попутного тангенциального точения, страница 6

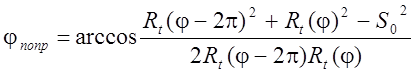.                                                            (3.12)

Тогда толщина среза a(j) определяется по формуле:

.                                                                          (3.13)

Теоретическое значение текущего радиуса R_tТ выражается формулой:

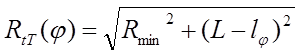,                                                                    (3.14)

где         l_j - величина перемещения точки А вдоль траектории движения подачи от момента касания инструмента с заготовкой до заданного момента времени.

Если принять, что скорость движения точки А равномерна и равна скорости движения подачи V_S, l_j можно определить по формуле:

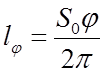.                                                                                             (3.15)

Однако, любая реальная система СПИД обладает конечной жесткостью. Поэтому в результате силового взаимодействия возникают деформации системы и вершина лезвия в результате перемещается на величину, отличную от l_j, что и вызывает искажение зависимости а(j) по сравнению с рассчитанной по формуле (3.14).

Пусть рассматриваемая система обладает жесткостью K_z и K_y вдоль осей z и y соответственно. Тогда отклонения т. А вдоль этих осей выражаются формулами:

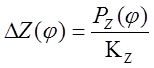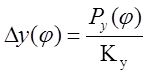,      ,                                                             (3.16)

где         P_z и P_y - проекции результирующей силы R на оси z и y соответственно (рис. 3.10,а).

В формуле (3.16) значение DZ соответствует величине К. Поэтому вершина лезвия вследствие деформации системы займет в действительности положение А’ (рис. 3.10). Следовательно, фактический текущий радиус R_tф из  треугольника А’ОВ (рис. 3.10,б) можно определить по формуле:

.                                                                  (3.17)

Полученное выражение позволяет рассчитывать мгновенное значение фактического текущего радиуса заготовки и при подстановке в формулу (3.13) получить действительный закон изменения толщины среза за цикл обработки ПТТ (рис. 3.7, кривая 3). Эта задача может быть решена при известных законах изменения сил P_z , P_y и величинах жесткости системы K_z и K_y. Значения P_z и P_y могут быть получены экспериментальным путем. При проектировании можно решать обратную задачу: по известным значениям сил (если имеется математическая модель) задать необходимые требования к жесткости соответствующих конструктивных элементов обрабатывающей системы.

1.5  Методика измерения действительной толщины среза

Обзор литературы [84, 148] и проведенные ранее исследования [58] показали, что изменение толщины среза в течение цикла обработки не соответствует теоретическому закону треугольника. Кроме того, установлено, что в цикле «резание» при ТТ доля проскальзывания, т.е. контакта заготовки с инструментом без образования стружки, достаточно велика и может достигать 20 % (см. рис. 4.6), что в значительной мере определяет механику образования стружки при ТТ.

Для измерения действительной толщины среза за цикл обработки  разработаны специальное устройство и методика, которая позволяет существенно повысить точность получаемого результата по сравнению с методикой, основанной на определении отклонения величины коэффициента укорочения стружки от его теоретического значения. Принцип действия предлагаемого устройства основан на непрерывном измерении величины воздушного зазора   между торцом неподвижно закрепленного датчика и поверхностью резания. Толщина среза определяется расчетным методом.

Для реализации этого подхода разработано устройство, состоящее из датчика индукционного типа, устанавливаемого на станке неподвижно относительно заготовки (рис. 3.1 и 3.11), и специального источника питания электрическим током, формирующего электрический сигнал для записи самописцем. Функциональная схема этого устройства приведена на рисунке 3.11,б.

Известно [[i]], что индуктивный датчик преобразует изменение величины зазора в изменение индуктивного сопротивления обмотки. Он работает на переменном синусоидальном токе частотой (для ферромагнитного сердечника) в пределах  2 - 10 кГц, выбираемой в зависимости от обрабатываемого материала. Основными элементами конструкции являются сердечник 1, катушка индуктивности 2, якорь 3 (рис. 3.12, а). При перемещении якоря изменяется воздушный зазор d, индуктивность катушки 1 и ее полное сопротивление переменному току

,                                                                                    ( 3.18)

где  и  - соответственно активное и индуктивное сопротивление катушки.

Чувствительность индукционного датчика определяется выражением [[ii]]:

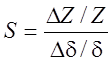,                                                                                ( 3.19)

т.е. обратно пропорциональна начальному зазору. Индукционные датчики особенно чувствительны при малых значениях воздушного зазора (до 1 мм). В литературе рекомендуются входные перемещения якоря в пределах от 0.01 до 5 мм.

Статическая характеристика датчика  (рис. 3.12, б) имеет изгибы в точках А и Б, поэтому величину первоначального зазора d₀ выбирают в середине прямолинейного участка. Кроме того, при переходе якоря через нулевого положение фаза выходного напряжения изменяется на 180°.