Необходимо определить оптимальные значения величин t1, t2 и t3 (Z1, Z2 и Z3) в зависимости от характеристик обрабатываемой поверхности, исходя из условия обеспечения одинаковой стойкости всех режущих элементов. Для этого проводим две серии опытов.
|
Рисунок 3.26 - Схема образования участков, формируемых на обработанной поверхности с радиусом Ri различными режущими элементами |
В первой серии экспериментов одну из заготовок, выбранную из партии случайным образом, многократно протачиваем на токарном станке, каждый раз удаляя слой металла, равный не более 20% общего припуска. По формуле (3.36) подсчитываем для каждого прохода показатель непрерывности обработки (HR)i
По результатам эксперимента строим график зависимости показателя непрерывности обработки (HR)i от величины расстояния Zi от поверхности заготовки.
После этого проводим вторую серию экспериментов и определяем влияние прерывистости обрабатываемой поверхности на работоспособность лезвия инструмента. Для этого одним из известных способов исследуем зависимость стойкости режущих элементов из выбранного инструментального материала от уровня прерывистости обработанной поверхности и глубины резания ti. С этой целью моделируем на заготовке из обрабатываемого материала условия прерывистого резания, т. е. искусственно создаем на заготовке участки сплошного материала и воздушные промежутки, причем эти условия назначаем таким образом, чтобы они соответствовали результатам первой серии экспериментов. Для реализации этого этапа исследований используем заготовки с заданным уровнем прерывистости (рис. 3.24).
Далее при постоянных значениях скорости резания и подачи осуществляем обтачивание заготовок с различными значениями (HR)i и глубины резания ti. Для получения зависимостей используются математические методы планирования экспериментов. Резание производим до достижения режущими элементом предельно допустимой (принятой) величины износа. После обработки результатов экспериментов получаем зависимости вида:
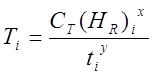, (3.40)
где Тi - стойкость режущего элемента;
СT - коэффициент, зависящий от обрабатываемого материала, скорости резания, подачи, материала режущих пластин;
х и у - показатели степеней при HR и t.
Исходя из того, что стойкость всех режущих элементов, установленных в резце, должна быть одинаковой, составляем систему уравнений:
|
Рисунок 3.27 - Ступенчатый резец с неравномерным распределением припуска между режущими элементами |
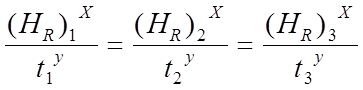, (3.41)
где t1, t2 и t3 - глубины резания, снимаемые режущими элементами соответственно 1, 2 и З.
Дополнительно к уравнениям (3.41) учитываем соотношения (3.42 и 3.43).
, (3.42)
, (3.43)
где åt - суммарная глубина резания (припуск на обработку), соответствующая расстоянию от поверхности заготовки до полученной в результате обработки поверхности с HR = 100%; СH - коэффициент, полученный в результате экспериментов по определению показателя непрерывности обработки. Решая совместно уравнения (3.41), (3.42) и (3.43),
определяем величины t1, t2 и t3, которые и реализуем в проектируемом инструменте (рис. 3.27).
Таким образом, согласно предложенному методу, поиск оптимальной схемы распределения припуска между режущими элементами осуществляется из условия постоянства для всех пластин отношения:
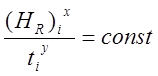. (3.44)
Пример определения оптимального варианта распределения припуска между лезвиями многоступенчатого резца при прерывистом (неравномерном) резании (на примере продольного точения) представлен в приложении Ж.
1.11 Методика теоретического анализ условий взаимодействия лезвия со срезаемым слоем при прерывистом резании
Чтобы уменьшить влияние упругих деформаций поверхностей на заготовке и элементов обрабатывающей системы и крутильных колебаний на ресурс инструмента при прерывистом (неравномерном) резании, в первую очередь необходимо путем регулирования режима нагружения лезвий изменением их геометрических параметров и конструкции инструмента на стадии его проектирования ослабить влияние трех факторов, определяющих динамическое состояние системы, а, следовательно, и характер нагружения рабочих поверхностей лезвий и режущих кромок: ударов при врезании инструмента, ударов при его выходе из зоны контакта с поверхностями на заготовке и крутильных колебаний, сопровождающих процесс прерывистого (неравномерного) тангенциального резания при обработке труднообрабатываемых материалов. Нами установлено, что можно существенно ослабить влияние этих факторов путем оптимального сочетания углов – переднего g, заднего a и наклона режущей кромки l.
При этом необходимо иметь в виду, что увеличение ресурса работы инструмента и уменьшение вероятности внезапных отказов путем изменения геометрических параметров лезвий, определяется не только динамичностью нагружения, но и величинами средних давлений, сил трения, температуры и времени контакта (рис. 2.3), существенно зависящими от значений переднего и заднего углов, угла наклона режущей кромки, углов в плане, остроты режущих кромок, схемы нагружения лезвий и инструмента и др. (см. разд. 2.2). Следует иметь в виду и то, что при оптимизации геометрических параметров лезвия, конструкции инструмента и условий его эксплуатации при прерывистом (неравномерном) резании, необходимо обязательно учитывать характер прерывистости обрабатываемой поверхности.
1.11.1 Анализ схемы взаимодействия лезвия со срезаемым слоем при обратном ударе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
