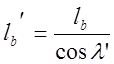 (3.58)
(3.58)
и, по аналогии,
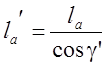 . (3.59)
. (3.59)
Уравнение передней поверхности в отрезках с учетом принятых знаков углов l и g в декартовой системе координат можно записать в виде (рис. 3.36):
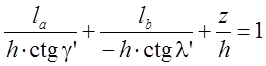 , (3.60)
, (3.60)
откуда
![]() , (3.61)
, (3.61)
где ![]() -
«текущее» заглубление лезвия в срезаемый слой.
-
«текущее» заглубление лезвия в срезаемый слой.
В любой рассматриваемой точке Н(В)ОП представляет
собой плоскость, параллельную оси ![]() и образующую угол
и образующую угол
![]() с осью
с осью ![]() (рис.
3.32). Из этих соображений получим следующее уравнение:
(рис.
3.32). Из этих соображений получим следующее уравнение:
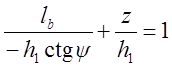 , (3.62)
, (3.62)
откуда
![]() , (3.63)
, (3.63)
где ![]() -
превышение точек с наименьшим диаметром над точками с наибольшим диаметром.
-
превышение точек с наименьшим диаметром над точками с наибольшим диаметром.
Таким образом, после подстановки система (3.64) примет вид:
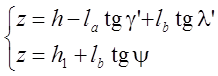 . (3.64)
. (3.64)
Решая эту систему уравнений относительно ![]() , получаем:
, получаем:
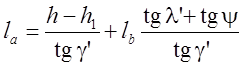 . (3.65)
. (3.65)
В зависимости от соотношения между g’, l’
и y, а, следовательно, и от
соотношения между g и l (при y=0о),
началом контакта (рис. 3.34) может быть плоскость ![]() ;
любой из отрезков
;
любой из отрезков ![]() или любая из точек
предполагаемой зоны контакта
или любая из точек
предполагаемой зоны контакта ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
Взаимосвязь между указанными параметрами геометрии лезвия
и положением нижней (верхней) ограничивающих поверхностей в системе координат ![]() можно представить параметром J - углом между положительным
направлением оси
можно представить параметром J - углом между положительным
направлением оси ![]() и вектором
и вектором ![]() . Его величина определяется из выражения:
. Его величина определяется из выражения:
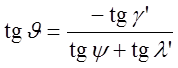 , (3.66)
, (3.66)
а в системе координат ![]()
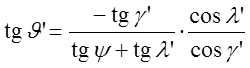 . (3.67)
. (3.67)
Необходимо учитывать, что J из выражения (3.66) принимает значения в пределах ![]() , в то время как действительное
значение J может находиться в
пределах от 0 до 2p. В связи с этим
выражение (3.66) представим в виде:
, в то время как действительное
значение J может находиться в
пределах от 0 до 2p. В связи с этим
выражение (3.66) представим в виде:
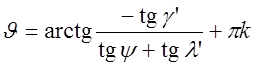 , (3.68)
, (3.68)
где 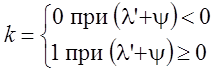 .
.
Необходимо отметить, что при g=0°, l=0°, y=0° выражение (3.68) неопределенно. Поэтому условимся, что в таком случае контакт начинается по всей зоне одновременно (рис. 3.34,а).
Начало контакта можно показать графически.
Рассмотрим случай при j=90°, j1=0° и y=0°. В этом случае зона контакта и сечение среза представляют собой прямоугольник A’B’C’D’ и прямоугольник ABCD соответственно (рис. 3.38,а).
|
а б Рисунок 3.38 - Проекция сечения среза на основную плоскость (а) и диаграмма определения начала контакта лезвия со срезаемым слоем (б) |
Здесь: ![]() - проекция главной
режущей кромки,
- проекция главной
режущей кромки, ![]() - проекция вспомогательной
режущей кромки,
- проекция вспомогательной
режущей кромки, ![]() - проекция вершины лезвия
на основную плоскость. Размеры сечения среза определяются значениями
- проекция вершины лезвия
на основную плоскость. Размеры сечения среза определяются значениями ![]() и
и ![]() .
Если принять, что вектор
.
Если принять, что вектор ![]() характеризует
направление перемещения линии пересечения НОП (Пвх, рис. 2.33) с передней поверхностью
характеризует
направление перемещения линии пересечения НОП (Пвх, рис. 2.33) с передней поверхностью![]() то, как видно из рис. 3.38,а, он может быть ориентирован в любом направлении. Это зависит от точки
начала контакта. Хорошо видно, что если контакт начинается в т.
то, как видно из рис. 3.38,а, он может быть ориентирован в любом направлении. Это зависит от точки
начала контакта. Хорошо видно, что если контакт начинается в т. ![]() , то угол J между положительным направлением оси
, то угол J между положительным направлением оси ![]() и
и
![]() изменяется от 0 до 90°, если контакт начинается из т.
изменяется от 0 до 90°, если контакт начинается из т. ![]() , то J изменяется от 90°
до 180° и т. д. по четвертям
координатной плоскости. Совмещая каждую из четвертей координатной плоскости с
, то J изменяется от 90°
до 180° и т. д. по четвертям
координатной плоскости. Совмещая каждую из четвертей координатной плоскости с ![]() так, чтобы соответствующая вершина
сечения среза (та, с которой начинается контакт в данной четверти) совпадала с
началом координат, получим диаграмму, представленную на рис. 3.38,б.
так, чтобы соответствующая вершина
сечения среза (та, с которой начинается контакт в данной четверти) совпадала с
началом координат, получим диаграмму, представленную на рис. 3.38,б.
На диаграмме буквы, расположенные около центра окружности внутри каждой из ее четвертей, обозначают вершину сечения среза, с которой начинается контакт. При этом буквы, расположенные вне окружности по ту же сторону от осей, обозначают прилежащие вершины сечения среза.
Видно, что про J=![]() , где
, где ![]() контакт
начинается по одной из сторон зоны контакта. Например: пусть l=5°,
g=10°, y=0°. Тогда
контакт
начинается по одной из сторон зоны контакта. Например: пусть l=5°,
g=10°, y=0°. Тогда ![]() и
и
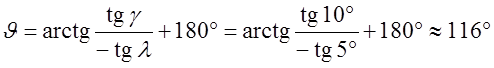 . Проводя вектор
. Проводя вектор ![]() под углом J=116°, определяем,
что он находится во второй четверти и, следовательно, контакт начнется в т. B,
принадлежащей главной режущей кромке K, и будет распространяться
вдоль нее (к вершине) и линии ВС, т.е. «вглубь» передней поверхности.
под углом J=116°, определяем,
что он находится во второй четверти и, следовательно, контакт начнется в т. B,
принадлежащей главной режущей кромке K, и будет распространяться
вдоль нее (к вершине) и линии ВС, т.е. «вглубь» передней поверхности.
Пусть l= -
5°, g=10°. Тогда ![]() и
и
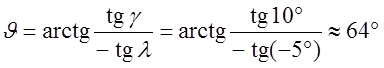 . Проводя вектор
. Проводя вектор ![]() под углом J=64°, определяем,
что он находится в первой четверти и, следовательно, контакт начнется в вершине
лезвия А и будет распространяться вдоль режущих кромок К и
К' от нее. Пусть l=0°, g=10°,y=0°. Тогда
под углом J=64°, определяем,
что он находится в первой четверти и, следовательно, контакт начнется в вершине
лезвия А и будет распространяться вдоль режущих кромок К и
К' от нее. Пусть l=0°, g=10°,y=0°. Тогда ![]() и
и 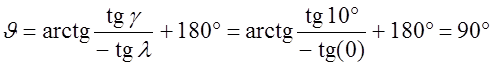 .
.
Проводя вектор ![]() под углом J=90°,
определяем, что он параллелен оси
под углом J=90°,
определяем, что он параллелен оси ![]() и контакт
начнется по всей длине главной режущей кромки и будет распространяться «вглубь»
и контакт
начнется по всей длине главной режущей кромки и будет распространяться «вглубь»![]() , т.е. первыми в контакт со срезаемым
слоем вступают точки
, т.е. первыми в контакт со срезаемым
слоем вступают точки ![]() , принадлежащие К,
и период врезания закончится по линии DC (рис. 3.34,б). При J=180° контакт начнется по ВС и линия
контакта будет перемещаться по
, принадлежащие К,
и период врезания закончится по линии DC (рис. 3.34,б). При J=180° контакт начнется по ВС и линия
контакта будет перемещаться по ![]() в направлении от
обрабатываемой поверхности к ВРК (рис. 3.34,в). При J=270°
контакт начнется по DC и линия контакта будет перемещаться к ГРК.
При J=360° контакт начнется по ВРК и линия контакта буде
перемещаться в направлении к обрабатываемой поверхности. Выход лезвия из
контакта со срезаемым слоем происходит в той же последовательности. Например,
первой из контакта при J=90° выйдет главная режущая кромка, а последней
– линия DС.
в направлении от
обрабатываемой поверхности к ВРК (рис. 3.34,в). При J=270°
контакт начнется по DC и линия контакта будет перемещаться к ГРК.
При J=360° контакт начнется по ВРК и линия контакта буде
перемещаться в направлении к обрабатываемой поверхности. Выход лезвия из
контакта со срезаемым слоем происходит в той же последовательности. Например,
первой из контакта при J=90° выйдет главная режущая кромка, а последней
– линия DС.
Необходимо отметить, что при ![]() ° даже при l=0° контакт будет точечным, в то время как при l=y
он начнется по линии. Например, пусть l=0°, g=10°, y=10°. Тогда
° даже при l=0° контакт будет точечным, в то время как при l=y
он начнется по линии. Например, пусть l=0°, g=10°, y=10°. Тогда ![]() и
и
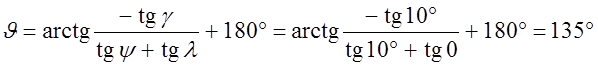 . Проводя вектор
. Проводя вектор ![]() под углом J=135°, определяем,
что он находится во второй четверти и, следовательно, контакт начнется в т. B,
принадлежащей K, и будет распространяться вдоль ГРК к
вершине и «вглубь» передней поверхности. Пусть l=0°, g=10°,
y=-10°.
Тогда
под углом J=135°, определяем,
что он находится во второй четверти и, следовательно, контакт начнется в т. B,
принадлежащей K, и будет распространяться вдоль ГРК к
вершине и «вглубь» передней поверхности. Пусть l=0°, g=10°,
y=-10°.
Тогда ![]() и
и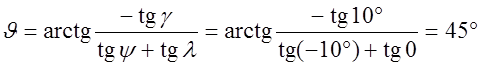 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.