Разработка методологии теоретико-экспериментальных исследований процессов нестационарного резания на базе попутного тангенциального точения, страница 16

Введем некоторые определения.

Сечение срезаемого слоя (сечение среза) – фигура, образованная при рассечении слоя материала заготовки, отделяемого лезвием за один цикл главного движения, статической основной плоскостью (ГОСТ25762-83).

В рассматриваемом случае представляет собой четырехугольник . Точка  - вершина; точка  - точка пересечения главной режущей кромки (ГРК) К и наружной образующей поверхности  заготовки в конце цикла главного движения резания; точка  - точка пересечения ГРК и наружной образующей поверхности заготовки в начале цикла главного движения резания; точка  - точка пересечения вспомогательной режущей кромки (ВРК) К' с поверхностью резания в начале цикла главного движения резания.

Боковые стороны этого четырехугольника являются следами граней четырехгранников среза (рис. 3.34). Очевидно, что их вид, положение и, соответственно, форма сечения среза зависят:  - от угла j и  ;  - от угла j₁ и ;  - от угла j и  ;  - от формы наружной образующей поверхности заготовки и .

Зона контакта – фигура, образованная при рассечении слоя материала заготовки, отделяемого лезвием за один цикл главного движения передней поверхностью. В рассматриваемом случае зона контакта представляет собой четырехугольник A’B’C’D’, точки A’, B’, C’, D’  которого принадлежат передней поверхности, а точки A, B, C, D являются  их проекциями на (рис. 3.34), т.е. сечение среза  является проекцией зоны контакта на основную плоскость. Анализ условий  контактирования лезвия инструмента с заготовкой будем выполнять по сечению среза.

Период врезания () – отрезок времени от момента касания лезвия со срезаемым слоем (срезом) до момента, соответствующего концу изменения (увеличения) площади контакта.

Период основного резания () – отрезок времени, характеризующийся постоянством площади контакта.

Период выхода () – отрезок времени от момента начала уменьшения площади контакта до момента выхода лезвия из контакта со срезаемым слоем.

Суммарное время резания () – общее время контакта лезвия инструмента с заготовкой за рабочий ход.

= ++                                                                              (3.54)

1.11.3  Определение зоны начала и конца контакта лезвия со срезаемым слоем при прерывистом резании

Для решения задачи рассмотрим статическую декартову прямоугольную систему координат . Направление и наименование осей выберем согласно рис. 3.35.

Начало координат  свяжем с точкой, наиболее приближенной к вершине (в вершине лезвия) в момент начала контакта.

Ось перемещений // (). Направлена в сторону вектора скорости резания в точке О, расположенной на лезвии инструмента.

Ось толщины среза  - ось в рабочей плоскости P_s, перпендикулярная оси  в точке  и направленная в сторону, противоположную движению подачи D_s.

Ось ширины среза  - ось в основной плоскости, перпендикулярная плоскости P_s (О) в точке  и направленная от оси заготовки.

Оси  образуют левую тройку векторов.

Кроме этого, введем косоугольную систему координат  так, чтобы плоскость была параллельна передней поверхности и . Во всем остальном эта система координат аналогична системе . Соотношения между координатами этих двух систем координат будут рассмотрены ниже. Для определения точки начала контакта (ТНК) введем следующие допущения: передняя поверхность лезвия  – плоскость; режущие кромки К и К'– прямые; радиус вершины лезвия  равен 0; радиус округления режущей кромки  пренебрежимо мал по сравнению с толщиной среза ; скорость резания, подача  и глубина резания  постоянны.

В любой момент периода врезания или выхода передняя поверхность пересекает нижнюю (верхнюю) ограничивающие поверхности. Согласно принятым допущениям передняя поверхность представляет собой плоскость .

Нижняя и верхняя ограничивающие поверхности в общем случае могут быть произвольными. Однако при практически применяемых глубинах резания, как указывалось выше, они могут быть аппроксимированы плоскостью ,что будет рассмотрено ниже.

Следовательно, две плоскости пересекаются по прямой, которая в процессе резания перемещается в плоскости сечения среза в направлении вектора , перпендикулярного ей. Этот факт можно записать в виде системы уравнений:

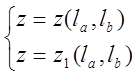.                                           (3.55)

Рассмотрим уравнения системы (3.55) подробнее.

С целью упрощения математических преобразований введем обозначения (рис. 3.36):

l’ – приведенный угол наклона режущей кромки – угол в сечении, перпендикулярном между следом передней поверхности и плоскостью .

g’ – приведенный передний угол – угол в сечении, перпендикулярном между следом передней поверхности и плоскостью .

Чтобы выразить эти параметры через статические главный передний угол g и угол наклона режущей кромки l, рассмотрим расчетную схему (рис. 3.37). Здесь плоскость  часть передней поверхности,  - часть режущей кромки,  - вершина. Плоскость  совпадает с . Плоскость  совпадает с плоскостью резания. Плоскость  совпадает с главной секущей плоскостью. Тогда из  можно записать:

,

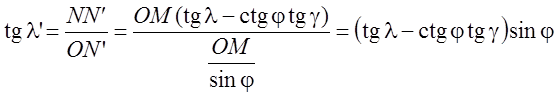где , .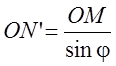

Таким образом,

.                                                                           (3.56)

Рассматривая аналогичную расчетную схему для переднего угла, получаем

.                                                                           (3.57)

Из рис. 3.37 так же можно отметить, что