Разработка методологии теоретико-экспериментальных исследований процессов нестационарного резания на базе попутного тангенциального точения, страница 14

Одной из существенных причин внезапного разрушения лезвия инструмента при прерывистом резании, кроме ударных нагрузок в момент врезания (входа) инструмента, циклического силового и теплового взаимодействия инструмента с заготовкой и специфичных условий резания ряда труднообрабатываемых материалов, являются ударные нагрузки в момент выхода инструмента из контактирующего с ним участка срезаемого слоя в результате упругого восстановления элементов обрабатывающей системы. Эти удары обусловлены тем, что при выходе инструмента из зоны резания система "станок – инструмент - заготовка", "сжатая" усилиями резания, восстанавливает свое исходное состояние, т.е. имеет место упругий возврат заготовки (инструмента) как в направлении, обратном главному движению резания (“раскрутка” системы), так и упругое восстановление в радиальном направлении, в т.ч. поверхностей на ней (резания и обработанной). В результате происходит обратный удар в зонах, прилегающих к режущим кромкам (главной и вспомогательной) со стороны задних поверхностей, что приводит либо к механическому разрушению лезвия, либо к образованию микро- и субмикротрещин, способствующих интенсивному его разрушению, вследствие свойственного для прерывистого резания циклического динамического и термического  напряженного состояния режущего клина. Анализ имеющейся по этому вопросу информации и наши исследования показали, что обратный удар является одной из главных причин внезапного отказа инструмента, особенно при прерывистой (неравномерной) обработке деталей из труднообрабатываемых материалов с малыми модулями упругости, т.е. склонных к упругопластическому последействию.

В момент выхода точки A из зоны резания (рис. 3.28) начинается процесс восстановления системы под действием упругих деформаций, соответствующих нагрузкам при установившемся  резании и жесткости элементов системы. При этом движение точки А будет сложным (в направлении вектора ) в результате упругого восстановления системы вдоль осей Y и Z со скоростями соответственно  и .

При восстановлении технологической системы из упругодеформированного состояния в исходное в направлении Y режущая кромка, перемещаясь по траектории главного движения в направлении оси Z, одновременно под действием упругих деформаций будет перемещаться на величину D и в направлении вектора скорости , что будет сопровождаться уменьшением заднего угла. Таким образом, траектория  движения точки A на заготовке относительно лезвия в результирующем движения со скоростью V_А определит значение величины a_D, на которую уменьшается задний угол a:

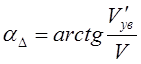                                                                                                     (3.45)

Следовательно, действительный задний  угол a₀ при выходе режущего клина из зоны резания будет равен a₀ = a - a_D  и зависит от соотношения скоростей резания и упругого восстановления технологической системы в направлении Y.

В зависимости от схемы нагружения лезвия и условий прерывистого (неравномерного) резания технологическая система  из упругодеформированного состояния в исходное положение может переходить либо по экспоненциальному  закону (в условиях мгновенного прекращения резания), либо по затухающему колебательному закону (в условиях, когда имеет место постепенное уменьшение действующих на лезвие нагрузок).

В первом случае:

,                                                                                         (3.46)

где         y - текущее значение упругой деформации D_I  в момент времени t  от начала выхода лезвия из зоны резания; T - постоянная времени экспоненты, характеризующая крутизну траектории точки А в движении упругого восстановления и зависящая от жесткости элементов системы и условий деформирования. Она численно равна постоянной демпфирования и колеблется в пределах 10^-4 – 10^-6 с [[vii]].

Скорость упругого восстановления в этом случае выразится формулой:

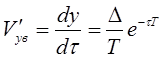.                                                                   (3.47)

Максимальная скорость упругого восстановления, при которой имеет место наибольшая потеря заднего угла, будет при t = 0, т.е. в момент начала выхода режущего клина из зоны обработки и равна

.                                                                                     (3.48)

Если упругая деформация D будет измеряться в мм, а постоянная времени в секундах, то для определения скорости в м/мин формула (3.48) примет вид:

.                                                                                                 (3.49)

С учетом этой зависимости из формулы (3.45) получим:

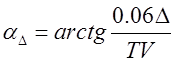, град                                                                                    (3.50)

В том случае, когда технологическая система из деформированного состояния в исходное положение возвращается по затухающему колебательному закону, скорость упругого восстановления можно характеризовать зависимостью:

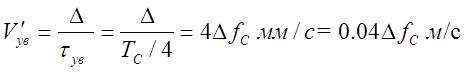,                                    (3.51)

где         t_ув - время упругого восстановления, с; T_С , f_C - соответственно период и частота собственных колебаний системы в радиальном направлении;

С учетом (3.51) формула (3.45) примет вид:

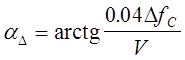, град                                                                    (3.52)

Из зависимостей (3.50) и (3.52) следует, что потеря заднего угла в значительной мере определяется величинами упругой деформации D на замыкающем звене и скорости резания V.