Разработка методологии теоретико-экспериментальных исследований процессов нестационарного резания на базе попутного тангенциального точения, страница 4

С целью получения результатов, учитывающих особенности тангенциального резания, введены понятия: средний коэффициент укорочения стружки за i-тый оборот заготовки () и усредненный коэффициент укорочения стружки за весь цикл обработки ().

Для определения коэффициента усадки стружки производится обработка (свободное резание) заготовок (рис. 3.3) с поясками шириной 2.5 мм, в которых просверлены диаметрально расположенные отверстия диаметром d_О = 0.8-1.0 мм на глубину несколько большую, чем величина снимаемого припуска После обработки каждого пояска, стружка тщательно собирается с целью определения действительной ее длины за цикл обработки. Длина стружки за цикл обработки и расстояние между отверстиями на ней измеряются с помощью тонкой медной проволоки Ǿ 0.2 мм. Следует отметить, что в исследуемом диапазоне режимов резания стружка, как правило, имеет вид непрерывной спирали. Для тех случаев, когда образуется элементная стружка, разработан бесконтактный метод определения коэффициента ее усадки (А.с. 870070 [114]).

Расчетная схема для определения теоретических значений длины стружки за цикл () и расстояний между отверстиями на соответствующем обороте () (без учета усадки стружки) за время контакта инструмента с заготовкой приведена на рисунок 2.4.

Траектория перемещения инструмента относительно обрабатываемой заготовки при попутном тангенциальном точении имеет вид циклоидальной кривой, характеризующейся текущим (мгновенным) значением радиуса поверхности резания , значения которого можно определить по формуле:

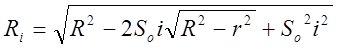,   (3.3)

где          - радиус обрабатываемой поверхности, мм;

 - подача инструмента, мм/об;  - порядковый номер оборота заготовки;  - радиус обработанной поверхности;

Мгновенное значение скорости определяется по формуле:

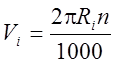.                   (3.4)

Теоретическое значение величины пути инструмента относительно заготовки за 1 оборот, определяем по формуле:

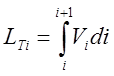.                                                                                           (3.5)

С учетом (3.3) и (3.4) это выражение принимает вид:

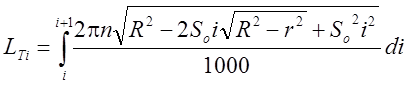.                                                             (3.6)

При этом теоретическая длина стружки за цикл обработки определяется, как:

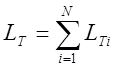,                                                                                           (3.7)

где  - число оборотов шпинделя за время контакта инструмента с заготовкой.

Сравнением теоретических () и действительных () значений длин всей стружки и расстояний между отверстиями () на соответствующем обороте заготовки можно определить:

- средний коэффициент укорочения стружки за i-й оборот:

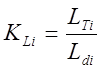;                                                                                                            (3.8)

- усредненный коэффициент укорочения стружки за весь цикл обработки:

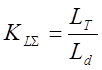 .                                   (3.9)

При проведении экспериментов заготовка закрепляется на оправке в шпинделе станка таким образом, что момент срезания участка с отверстием совпадает с появлением сигнала датчика оборотов заготовки. Этим достигается фиксация порядкового номера оборота , на котором произошло срезание участка с отверстием, и соответствующего ему действительного значения длины образовавшейся стружки.

Обработка результатов, полученных таким образом, дает возможность построить график изменения коэффициента укорочения стружки на каждом обороте цикла обработки (рис. 3.5).

1.4  Методика теоретического анализа кинематики процесса попутного тангенциального точения

Как неоднократно отмечалось, одной из специфических особенностей процесса попутного тангенциального точения является переменная толщина среза за цикл обработки.

При обработке заготовки 1 методом ПТТ (рис. 3.6) вершина лезвия инструмента 2 движется по траектории ВС, являющейся касательной к обработанной поверхности, со скоростью подачи V_s.

При этом траекторией относительного движения инструмента является циклоидальная кривая. При прохождении участка ВА (участок контакта инструмента с обрабатываемой заготовкой) с равномерной скоростью подачи V_s (рис. 3.6), теоретическое значение толщины среза в течение цикла обработки изменяется по закону треугольника (рис. 3.7, кривая 1) с максимумом в конце первого оборота заготовки.

Так как отношение 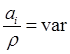 () и может изменяться за цикл обработки от 0 (при ), когда резание отсутствует (2.19), до максимального значения (при ), то действительный закон изменения толщины среза в течение цикла обработки отличается от теоретического и может быть представлен четырьмя характерными участками, два из которых (в момент входа и выхода инструмента из контакта с заготовкой) характеризуются проскальзыванием, т.е. отсутствием резания, интенсивным трением задней поверхности лезвия о заготовку и упрочнением срезаемого слоя и поверхностного слоя детали, что в значительной мере предопределяет как работоспособность инструмента, так и качество обработанной поверхности при ПТТ. В процессе изучения явления проскальзывания установлено [132], что его удельный вес в цикле обработки ПТТ может превышать в зависимости от условий обработки 20% (см. рис. 4.6). Это обстоятельство вызывает необходимость изучения процессов, происходящих на тех участках цикла, которые характеризуются  проскальзыванием.