Electrochemistry of Room-Temperature/ Articles about substances designated as ionic liquids have begun to appear with increasing regularity in chemistry journals around the world, страница 13

The various electrochemical techniques that have been used to probe electrochemical reactions are discussed in detail in many excellent comprehensive texts and monographs. This Section is intended as an aid for those researchers who are interested in doing electrochemistry in RTILs, but do not have research experience or academic training in electrochemistry. Brief descriptions of some of the more popular techniques are described here along with references to examples of studies in ionic liquids where these techniques were effectively employed.

(i) Cyclic Voltammetry

Cyclic voltammetry (CV) is widely employed as a survey technique, i.e., it is the first technique that is commonly applied during the preliminary analysis of an electrochemical system. With the demise of analog signal generators, true analog sweep cyclic voltammetry has been largely supplanted by cyclic staircase voltammetry (CSV). This technique varies from analog sweep voltammetry in that the potential is changed in small steps. As long as the step size is sufficiently small, the theories developed for CV can be applied to CSV.^321,335 The correct analysis of cyclic voltammetric data is somewhat of an art, and there are many examples of investigations where such CV data have been grossly overinterpreted or misinterpreted altogether.

If the electrochemical reaction (oxidation or reduction) is a simple diffusion-controlled process, i.e., an electrochemically reversible or Nernstian system in which charge transfer is very fast so that the reaction rate is limited by the rate of diffusion of the soluble electroactive species to the electrode surface in the test solution, then, the absolute magnitude of the voltammetric peak current, i_p, is given by the well known Randles-Sevick equation:³²¹

n3/2F 3/2 1/2 * 1/2   ip = 0.4463 1/2 1/2 AD Cν (6) R T

where A is the electrode area (cm²), C^* is the bulk solution concentration (mol cm^-3), D is the diffusion coefficient of the electroactive species (cm² s^-1), n is the number of electrons involved in the reaction, ν is the potential scan rate (V s^-1), and all of the other symbols have their usual meaning. Linear plots of i_p as a function of v^1/2 that pass through the origin suggest that the system under study is diffusion controlled. However, this is not a definitive test because the same behavior is also observed for an irreversible electrode reaction.³³⁶ Fortunately, there are other criteria that can be examined in order to verify the reversibility of the system under study. For example, the peak potential for the oxidation or reduction wave in question is independent of scan rate in the case of a reversible system, but varies with scan rate for a quasi-reversible or irreversible systems. Likewise, the nonlinearity of a plot of i_p versus ν^1/2 does not necessarily indicate a slow charge transfer process. It may simply indicate that the electrode reaction rate is governed by the rate of a chemical reaction preceding the chargetransfer step.³³⁶ If n, C^*, A, and T are known and the system in question has been proven to be electrochemically reversible, then D can be estimated from the slope of a plot of i_p versus ν^1/2 by using Eq. (6).

For a reversible (Nernstian) reaction, the following criteria are valid

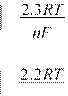
                                      Epa − Epc =                                                (7)

                                      Ep − Ep/2 =                                                 (8)

                                                             nF

where E_pa, E_pc, and E_p/2 are the anodic peak potential, cathodic peak potential, and the appropriate half-peak potential, respectively. E_p/2 is simply the potential at 50% of i_p. When the reaction is known to be reversible, the number of electrons involved in the reaction can be estimated from Eqs. (7) and (8).³²¹ Note, however, that Eq. (7) varies slightly with changes in the voltammetric switching potential. Thus, Eq. (8) is probably superior to Eq. (7) for estimating n. For a reversible electrode reaction, the voltammetric half-wave potential, E_1/2, can be determined by estimating the potential at which 85.17% of the peak current is observed.³³⁶ E_1/2 can also be estimated from the relationship given in Eq. (9):