Сущность, принципы и требования к управленческим решениям. Виды управленческих решений. Технология принятия решений, страница 5

При выборе конкретного класса функций для аппроксимации функции ценности стоит обратить внимание на то, что линейная функция ценности соответствует случаю, когда предельная ценность постоянная. Квадратичная функция ценности может применяться в случаях, когда предельная ценность или убывает или возрастает. Кубическая функция ценности может воспроизводить и более  сложные ситуации – когда, например, маржинальна ценность сначала убывает, а затем возрастает, или наоборот – сначала возрастает, а затем убывает (такие функции абсолютной ценности получили название  - подобных).

Задача 1. Для уменьшения текучести кадров на предприятии были предложены следующие альтернативные решения. Введение надбавки к тарифной ставке за непрерывную работу (текучесть уменьшилась до 15%). Проведение активной корпоративной компании (текучесть уменьшилась до 14%). Возможность повышения квалификации за счет предприятия после 5 лет непрерывной работы (до 12%). Приобретение 1% акций предприятия после каждых двух лет непрерывной работы на предприятии (до 11%).

Постройте интервальную функцию ценности на множестве приведенных альтернатив, определите ценность каждой альтернативы, примите наиболее ценное административное решение.

Начальная текучесть кадров до внедрения изменений на предприятии составила 18%.

Решение. 1) пусть ценность в критических точках равняется: ;

.

2) определим прибыль в критических точках и половинных точках методом половинного деления:

2.1. Начальное состояние: . Конечное состояние: .

2.2. ; ; ; ; ; ; ; .

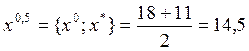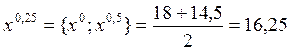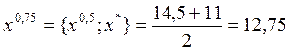2.3. Контроль: ;  .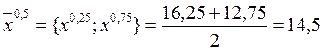

2.4. Присвоим соответствующие ценности:

; ; .

3) найдем линейную аппроксимирующую функцию ценности, для чего воспользуемся МНК.

3.1.Решим систему уравнений: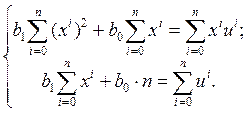        (3.7)

Все результаты вычислений занесем в таблицу:

Таким образом получим систему уравнений:

Откуда  . Следовательно, линейная аппроксимирующая функция ценности имеет вид: .

Для определения адекватности модели рассчитаем коэффициент детермінації, который сравнивает фактические значения функции и значения полученные из уравнения аппроксимирующей функции.

Коэффициент детермінації  вычисляется по формуле:

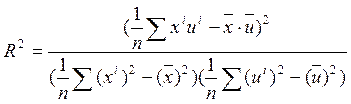 .          (3.8)

Если  (), то это полная корреляция и нет  разницы между фактическими и смоделированными данными.

Если , то неправильно подобранно уравнение регрессии.

По формуле 3.8. .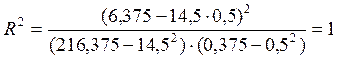

Воспользовавшись подпрограммой „Мастер диаграмм” табличного процессора Excel можно определить аппроксимирующую функцию ценности (линейную, квадратичную, кубическую) :