Сущность, принципы и требования к управленческим решениям. Виды управленческих решений. Технология принятия решений, страница 10

 - множество допустимых планов, отдельный элемент которого обозначен через .

Допустимые планы сравниваются сопоставлением оценок, причем оценка произвольного допустимого плана многокритериальной задачи является векторной: .

Исследование многокритериальной задачи и проработку методики многокритериальной оптимизации удобно проводить, если рядом с исходной многокритериальной задачей рассмотреть такую вспомогательную одинкритериальную задачу:

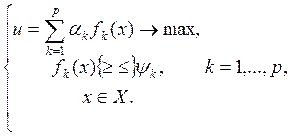              (3.4)

где,   - некоторые действительные числа, причем знаки первых из них, а также знаки неравенств в критериальных ограничениях согласовываются с оптимизационной направленностью (к максимуму или к минимуму) соответствующих целевых функций.

Обобщенная методика многокритериальной оптимизации состоит из нескольких этапов. Рассмотрим последовательное описание каждого из них.

Этап 1. Отсев неэффективных планов и определение (или приближенное оценивание) пределов вариации каждой из целевых функций на множестве эффективных планов.

Если для каждой из целевых функций ее наилучшее значение на множестве эффективных планов  совпадает с ее наихудшими значениями на этом множестве  ( для всех ), то делаем вывод, что все эффективные планы равноценные. Произвольный из них может быть выбран за решение задачи.

В типичном случае, который и требует последующей проработки, по крайней мере для двух целевых функций будет выполняться неравенство . Оставим в составе критериальных лише эти функции. Все другие целевые функции на множестве эффективных планов, можно отбросить, если отбросить вместе с ними и те допустимые планы, которые не отвечают наилучшему уровню этих целевых функций (отбрасывание обеспечивается введением дополнительных ограничений типа ; в дальнейшем будем считать, что эти ограничения уже присутствуют в описании множества ).

Результат. Пределы вариации   по каждой из целевых функций, где ззвездочкою обозначено наилучше, а нулем – наихудшее значение – й целевой функции на множестве эффективных планов.

Этап 2. Построение обобщенной адитивної функции ценности:

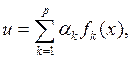                          (3.5)

где весовые коэффициенты вычисляются без участия ЛПР по формулам

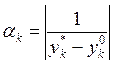, ,                       (3.6)

или, если есть возможность общения из

ЛПР на этом этапе, по результатам следующего диалога:

1). ЛПР получает  профилей типа , ,...,, но должен определить среди них наилучший.

Допустим, что лучшим будет первый профиль: 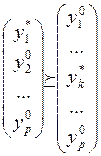 для всех (знак соответствует отношению „не хуже” по системе предпочтений ЛПР). 2). Для каждого из профилей , , ЛПР должно указать такое значение  первой целевой функции при котором профили и  считаются равноценными. (Очевидно, что  для всех ).

3). На основе ответов ЛПР о значении , составим систему соотношений для весовых коэффициентов :

,

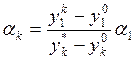Пусть 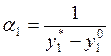, после чего окончательно получаем:

, .

Примечание. Если весовые коэффициенты были вычислены без диалога с ЛПР, то это отвечает предположению, что все профили, если бы они сравнивались, оказались бы равноценными, то есть что  для всех  . К тому же, конкретные значения весовых коэффициентов мало влияют на окончательный результат, потому на этом этапе диалог с ЛПР хотя и желателен, но не обязателен.

Результат. Обобщенная адитивна функция ценности:

.

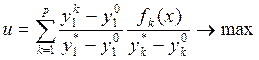Этап 3. Отыщем такой допустимый план, который отвечает максимуму обобщенной адитивної функции ценности:

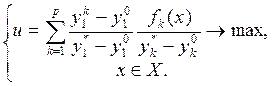
Этот план является эффективным. Его оценка вместе с пределами вариации   показателей передается ЛПР.

Результат. Оценка плана  в пределах вариации каждой из целевых функций на множестве эффективных планов.

Этап 4. ЛПР или соглашается выбрать план  за решение многокритериальной задачи, или  по каждой из целевых функций указать такие допустимые уровни, которые  считает удовлетворительными.

Примечание. Нужно предупредить ЛПР о необходимости придерживаться требования  для всех . Если ЛПР некоторые из критериев оставляет вне поля зрения, то для них  .