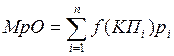Сущность, принципы и требования к управленческим решениям. Виды управленческих решений. Технология принятия решений, страница 15

                        (4.24)

где  - дегресивно растущая функция полезности;  – стоимость капитала  – го состоянию среды; – вероятность наступления  – го состоянию среды.

На відміну від критерію середнього значення  та стандартного відхилення у величині корисності трансформуються можливі результати. Альтернатива з максимальним значенням  математичного сподівання корисності є оптимальною. Якщо відношення до ризику нейтральне, цей критерій відповідає правилу Байєса.

Критерий Лапласа позволяет отделить кращий вариант в том случае, если ни одно из условий не имеет существенного преимущества.

Коли не має ніяких підстав вважати, що кожний окремий стан природи більш імовірний, порівняно з іншими, використовують припущення, що ймовірність виникнення кожного з можливих станів навколишнього середовища однакова. Такому випадку цінності кожної альтернативи можна обчислити за формулою звичайного середнього арифметичного всіх її  можливих оцінок у різних станах природи. Оптимальною є та альтернатива, яка має найбільшу середню оцінку 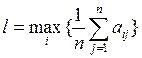 [3, c.118].

Критерий Ходжеса – Лемана основывается на сочетании критериев Байеса и Вальда за помощью (): оптимальной считается стратегия, что отвечает условию:

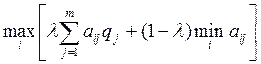.               (4.25)

При  получают критерий Вальда, при  – критерий Байеса [4, c.300 - 301].

Задача 1. В городе Чернигове фирма СТТ планирует строительство овощехранилища. Имеются три возможных проекта площадью: 200 ; 300 ; 400. В зависимости от эффективности использования выделенных площадей рассчитанны варианты дохода за каждый год (тыс. грн.), которые предоставлены в платежной матрице таблица:

Платежная матрица

	Доход от использованной площади (тыс. грн.)
	из 100 м2	из 200 м2	из 300 м2	из 400 м2
200	130	350	350	350
300	60	410	520	520
400	-140	290	560	670

Необходимо определить наиболее целесообразный вариант строительства.

Решение.  Анализ игры начнем с критерия Вальда. По формуле (4.) имеем: .

Наиболее надежным является построение  овощехранилища .

По оптимистическому критерию:

.

Отже, найбільш ризикованим є вибір .

Критерий Гурвица при параметре  дает такие результаты:

.

Критерий Лапласа:

.

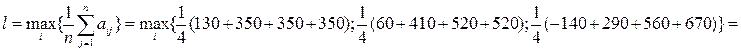
За вибором ОПР, з урахуванням критеріїв оптимальності, найкращою альтернативою є побудова овочесховища площиною 400 м².

Задача 4. Магазин имеет некоторый запас товаров ассортиментного минимума. Если запас товаров является недостаточным, то необходимо завезти его с базы, если запас превышает спрос, то магазин несет расходы по хранению нереализованного товара. Пусть спрос на товары  лежит  в пределах 5-8 единиц, расходы по хранению одной единицы товара 0,1 грн., расходы на доставку товару 0,2 грн. Определить оптимальную стратегию магазина по завозу товаров. Составить платежную матрицу.

Решение. Элементы матрицы определяются следующим образом: если магазин имеет 5 единиц одного товара и спрос равняется 5, то магазин имеет расходы и элемент .

Если магазин имеет 6 единиц товара, а спрос равняется 5, то магазин может продать  5 единиц товара, а 1 единицу товара должен хранить, имея при этом расходы, которые определяются элементом .

Если магазин имеет 5 единиц товара, а спрос равняется 6, то магазину необходимо завезти 1 единицу товара, тратя для этого сумму 0,2 грн. Следовательно, элемент . Проведем аналогичные размышления и одержимо значения всех элементов платежной матрицы:

Платежная матрица