Сущность, принципы и требования к управленческим решениям. Виды управленческих решений. Технология принятия решений, страница 11

Результат.Необходимо ли продолжать процесс поиска решения: набор допустимых уровней  .

Этап 5. Определяется реальность определенных на этапе 4 допустимых уровней критериальных показателей и осуществляется их коррекция или в сторону улучшения, если они являются реальными, или в сторону послабления, чтобы сделать реальными. Для этого решают такую одинкритериальную задачу:

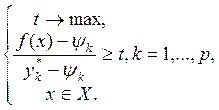
Примечание. Для целевых функций, направленных к максимуму, выполняется неравенство, потому критериальное ограничение приобретает вид: . Для направленных к минимуму целевых функций критериальное ограничение является несколько другим: .

Из-за отсутствия абсолютно–оптимальных планов оптимальное значение  параметра  менее 1. В то же время замечаем, что  для всех  при . Случай  свидетельствует о реальности допустимых уровней, а случай – об их нереальности. Реальные допустимые уровни  определяются путем сравнения величин  и , и выбору из каждой такой пары наилучшей.

Результат. Вывод о реальности или нереальности первичных допустимых уровней (значение ) и установление реальных допустимых уровней , .

Этап 6. Разыскивается такой эффективный план, который отвечает реальным допустимым уровням всех критериальных показателей. Он является решением одинкритериальной задачи:

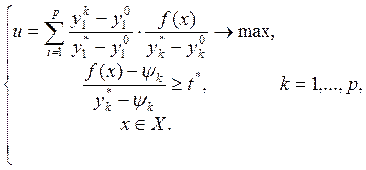
Результат. Вывод о реальности или нереальности первичных допустимых уровней (значение ), реальны допустимые уровни , , а также оценка  с рекомендацией об утверждении плана  как решении многокритериальной задачи. Вся эта информация посылается ЛПР.

Этап 7. Если ЛПР не соглашается с рекомендацией выбрать эффективный план  за решение многокритериальной задачи, то надо осуществить коррекцию первичных допустимых уровней целевой функции . Для обеспечения сходимости метода новые уровни ,  должны быть слабее чем предыдущих.

Результат. Или делаем вывод о завершении процесса, или возвращаемся к этапу 5, учитывая новые значения допустимых уровней целевых функций .

Задача 3. Информация о 8 альтернативных маршрутах подана в таблице. Критериями выбора является время и стоимость (с оптимизационной направленностью каждого показателя к минимуму).

Таблица 3.5

Показатели транспортных маршрутов

Определить наиболее привлекательный маршрут при оптимизации направленной к минимуму с помощью построения функции ценности.

ЛПР считает, что эффективные допустимые уровни мин, коп, проверить являются ли они реальными и предложить наиболее близкое решение к допустимому.

Решение. Этапы 1-2. Считают, что все маршруты эффективны.

Этап 3.Характеристика множества эффективности маршрутов и определение весовых коэффициентов ФЦ.

,

.

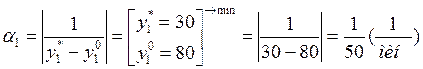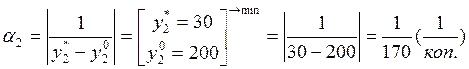Следовательно, целевая функция имеет вид: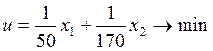, где  (, ) - время, мин; (, ) - стоимость, коп..

Вычислим ценность каждого маршрута, результаты  расчетов приведены в таблице:

Расчетные показатели транспортных маршрутов

Наилучший показатель ценности имеет четвертый маршрут: