Сущность, принципы и требования к управленческим решениям. Виды управленческих решений. Технология принятия решений, страница 14

4)  выбираем решение, при котором максимальный риск будет меньше, чем при других решениях .

Критерий используется тогда, когда необходимо выбрать стратегию защиты объекта от слишком больших расходов. Использование критерия Севиджа целесообразно только при условии достаточной финансовой стабильности предприятия, когда есть уверенность, что случайный убыток не приведет к полному краху [3, c. 87].

Компромисом к минимаксным підходів є метод Гурвіца, коли два екстремальних сценарії (найгірший і найкращий) ураховуються спільно. А за ваговим коефіцієнтом у згортці сценаріїв є параметр  (), значення якого задається особою, яка приймає рішення, за суб’єктивними міркуваннями. Чим більше значення набуває  , тим оптимістичніше налаштована особа, яка приймає рішення [2, c.150].

Оптимальной за критерием Гурвица считается чиста стратегия найденная из условия :

 или .

Для поиска оптимальной стратегии за критерием Гурвица рекомендуют два подхода:

- находят рекомендовані стратегії з умов оптимізму () і песимізму (). Якщо в обох випадках отримана одно стратегія, то вона є оптимальною. Якщо отримують дві стратегії, то на основі схильності чи несхильності гравця до ризику формується чиста (оптимістична чи песимістична) або змішана стратегія;

- рассматривают варианты крайнего оптимизма (k=0) и пессимизма (k=1). Если расчеты предлагают две стратегии, то определяют момент изменения стратегии, приравняв выражения за ними (), и решают уравнение относительно  к.

4.6 Критерії оптимальності в умовах ризику

Здійснюючи оцінювання, приймаючи рішення в умовах ризику, зумовленого невизначеністю, відсутністю повної (числової) інформації, неможливо повністю уникнути певного суб’єктивізму. А тому прийняття оптимальних (раціональних) економічних рінь має здійснюватись за умов мінімального рівня суб’єктивізму і раціонального (прийнятного) рівня ризику [1, c.139].

Найбільш ефективними критеріями прийняття рішень в ігрових моделях є: правило Байєса (критерій математичного сподівання), критерій середнього значення і стандартного відхилення, критерії Бернуллі, Лапласа, Гурвіца тощо. Якщо критерії свідчать, що необхідно прийняти одне й те саме рішення, то це підтверджує його оптимальність. У разі зазначення на різні рішення пріоритет варто віддати тому з них, у якого більше математичне сподівання. У ситуації ризику він є основним [3, c.117].

Правило Байєса (критерій  математичного сподівання) грунтується на припущенні, що відомі ймовірності настання можливих станів зовнішнього середовища ().

Обязательное требование – 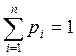. Она значит, что использованы все возможные состояния природы и других быть не может. Критерием выбора является значение математического ожидания альтернативы .

В соответствии с правилом Байеса оптимальной считается альтернатива с большим значением математического ожидания, чем в других альтернативах.

Критерій середнього значення і стандартного відхилення. Для оцінки розсіювання значень критерію (обраного параметра) щодо його середнього прогнозованого значення математичного сподівання доцільно використовувати таку характеристику, як дисперсія – стандартне відхилення результатів (вартості капіталу) як ступеня ризику у критерії прийняття рішень.

Чим вище стандартне відхилення, тим більший ризик. Для запобігання ризику особа, що приймає рішення, вибирає із двох альтернатив з однаковими  математичними сподіваннями альтернативу з найменшим стандартним відхиленням (дисперсією).

Критерій Бернуллі. За обгрунтуванням Бернуллі можлива зміна  значень математичних сподівань і моментів ризику цільових функцій (наприклад вартості капіталу) на очікувану корисність (вигоду).

Замість монетарних цільових функцій використовується корисність, і особа, яка приймає рішення, пов’язує її з цілями, очікуваним ступенем їх досягнення, врахуванням відношення ризику. У цьому випадку виходять із того, що особа, яка приймає рішення, може оцінити вигоду (корисність) різних альтернатив і вибрати максимум „морального очікування” (), розраховуючи його за такою формулою: