Сущность, принципы и требования к управленческим решениям. Виды управленческих решений. Технология принятия решений, страница 4

В принятии решений особая роль принадлежит таким допустимым планам  из множества Х, которые при заданном отношении предпочтений  „не хуже” были наиболее предпочтительными по сравнению с другими допустимыми планами:

, , ,

поскольку именно они определяют решение задачи с точки зрения конкретного ЛПР.

Такие планы называют также максимальными при отношении  предпочтений    „не хуже” ().

Для численной оценки  множества планов  (альтернатив) которые определяются семьей І отношений предпочтений, первичным является отношение  „не хуже” ().

Функцией ценности называется такая действительная функция :, определенная на множестве, которое отвечает условию

      .         (3.1)

Это значит, что план , не хуже, чем план  тогда и только тогда, когда ценность  плана  не меньше ценности  плана .

Таким образом, функция ценности  отображает на множестве отношение предпочтения . Для двух других основных отношений предпочтения это отображение осуществляется таким образом:

„равноценно”:         ;

„лучше”:        .

Функция ценности, единственная с точностью до произвольного монотонно растущего преобразования  , , где  - функция ценности, а  - любая возрастающая функция действительной переменной - называется порядковой. Когда же есть некоторая дополнительная информация об отношении предпочтения, а функция ценности, которая отображает это отношение, остается единственной только с точностью до произвольного положительного линейного преобразования, , где , , то ее называют интервальной.

Ее особенность заключается в том, что она в отличие от порядковой, позволяет определить не только то, что один план более предпочтителен от другого, а еще и характеризует то, на сколько отличаются элементы между собой по предпочтительности.

Если функция ценности  полоржительна и единственна  с точностью до произвольного положительного множителя , то есть когда возможным остается только преобразование, , ,то такую функцию называют относительной.

Относительная функция ценности показывает, во сколько раз один элемент более предпочтителен, чем другой.

Построение интервальной функции ценности (ИФЦ) на одномерном множестве применяется при выборе отношений предпочтения и их численной оценки.

ИФЦ определяется в том случае, когда отношение предпочтения изменяется монотонно и эта монотонность является постоянной, то есть: .

Методика построения ИФЦ состоит из двух этапов

Этап 1. Определение точечных оценок функции ценности методом половинного деления

Если в предельных точках промежутка  значения функции ценности еще не определены, то полагают:, . Это условия нормирования (или начальные условия) функции ценности.

1.1. На промежутке    находим половинную по ценности на этом промежутке точку  .

1.2. На промежутке  находим половинную по ценности на этом промежутке точку .

1.3. На промежутке   находим половинную по ценности на этом промежутке точку .

1.4. (контрольный). На промежутке  находим половинную поценности на этом промежутке точку .

Сравниваем   и  , если они почти не отличаются, то проверку считают успешной и переходят к следующему шагу. Если существует существенное расхождение между значениями  и , то необходимо повторить шаги 1-4 с целью уточнения точек, половинных по ценности на соответствующих промежутках. При необходимости процесс может быть продолжен  для получения точек  .

1.5. Присвоим соответствующие ценности половинным точкам. Для этого  буденм считать, что: ; ;  и фиксируем эти результаты.

Этап 2. Выбор аппроксимирующей функции предпочтений проводится с помощью построения графика  и выбора по критерию максимальной достоверности аппроксимации конкретного вида функции:

1) линейной ;

2) квадратичной ;

3) кубической, и тому подобное.

При выборе аппроксимирующей функции полезно принимать во внимание маржинальну (предельную) ценность. Маржинальной  ценностью называется производная функции ценности:

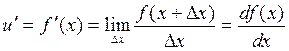.                (3.2)