Общие вопросы принятия решения. Сущность принятия решений, его проблемы. Классификация решений, страница 22

Наиболее трудоемким процессом является принятие решения сложных задач, которые принимаются в условиях риска и неопределенности. Под риском следует понимать потенциальную изменчивость объективных характеристик объекта или явления. Для его учета применяется теория вероятностей, математическая статистика, методы исследования операций. Одним из часто используемых инструментов в таком случае может быть матрица результатов.

Обозначим объективные условия через Y_j , где j – количество различных объективных условий (затраты капитальные и текущие, показатели качества, время и т.п.) – может принимать значения от 1 до n . Варианты решений (стратегий) обозначим через С_i , где i – количество вариантов  (пайка, сварка, крутка, опрессовка и пр.) – может принимать значение от 1 до m. Результат, ожидаемый при каждом сочетании вариантов решений и объективных условий, обозначим через Q_ij . Тогда матрица результатов решений при n=3 , m=4 будет иметь вид:

Таблица 4

Матрица результатов решений

Универсальность матрицы результатов решений заключается в том, что она может быть использована при решении самых разнообразных производственных задач. Объективные условия в матрице отражают нерегулируемые факторы, которые могут оказать влияние на результаты решений, а показатели результата характеризуют то, что будет достигнуто при выборе данного варианта решения и возникновения определенных объективных условий.

Матрица результатов позволяет осуществлять выбор решений в условиях риска, так как в ней учитывается вероятность появления тех или иных объективных условий.  Если обозначить через Р – вероятность их возникновения, то сумма вероятностей возникновения возможных условий очевидно равна единице:

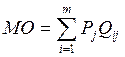, то есть среднее значение результатов варианта решения равняется сумме произведений каждой из величин результатов по всем рассматриваемым объективным условиям на соответствующие вероятности их возникновения (по строчкам матрицы). Поиск наилучшего решения в данной трактовке проблемы возможен с применением теории игр с привлечением аппарата линейного программирования, рассматриваемого в курсе «Методы оптимизации». Решение возможно в виде смешанной стратегии.

Наиболее осторожные руководители обычно стремятся избегать какого-либо риска и выбирают тот вариант решения, который обеспечивает минимальные потери при неблагоприятно сложившейся обстановке – правило минимизации максимального убытка, рассматриваемое в теории игр как теорема о минимаксе. 

Руководитель-оптимист часто стремится выбрать такой вариант решения, который дает наилучший из всех лучших результатов, несмотря на то, что при неблагоприятных условиях он может понести большие потери. Этот результат называется максимаксом.

Теория игр - это математический метод планирования действий в конфликтных ситуациях. В настоящее время она достаточно полно разработана только для частного случая игры двух противников с противоположными интересами и с нулевой суммой платежей.

Применение матричной записи результатов возможных решений позволяет сформулировать несколько видов критериев.

   Максиминный критерий. Для выбора варианта действий по этому критерию поступают следующим образом. В каждой строке находят минимальное значение Q _j и таких величин будет ровно m. Из этого ряда минимальных значений выбирается максимальное значение результата Q_ij и этот вариант решения может быть принят. Особенностью максиминного критерия является то, что он ориентирует на выбор наиболее безопасного варианта. Это своего рода критерий осторожного человека, так как при любом из рассмотренных вариантов условий результат действий будет не хуже минимума.