Пункт 1. Решение задачи при помощи модуля ПОИСК РЕШЕНИЯ.
Нам необходимо отобрать проекты таким образом, чтобы суммарная чистая текущая стоимость отобранных проектов была максимальна и при этом, чтобы в каждом году суммарные инвестиции, требуемые для финансирования отобранных проектов, не превышали выделенных сумм Bk .
Модуль ПОИСК РЕШЕНИЯ является надстройкой. Если он не установлен на компьютере, то необходимо вызвать СЕРВИС – НАДСТРОЙКИ – установить метку ПОИСК РЕШЕНИЯ – ОК (см. рис. 1.2) [1]. Далее вызываем команду СЕРВИС – ПОИСК РЕШЕНИЯ[2] (рис. 1.4). Установить целевую ячейку: В9, равной: максимальному значению, ограничения: ДОБАВИТЬ. Появится меню ДОБАВЛЕНИЕ ОГРАНИЧЕНИЯ
(рис. 1.3). Ссылка на ячейку: С9:G9 – это левые части ограничений, которые должны содержать формулы, выбираем знак – в нашем случае «≤», ограничение: C10:G10 – это правые части ограничений, в которых должны быть числа. Нажимаем кнопку ДОБАВИТЬ и вводим ограничение на переменные: Н3:Н8 = двоич. – ОК.
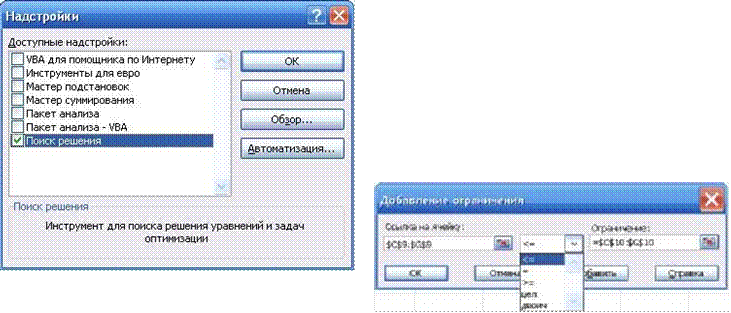 Рис.
1.2. Установка надстройки
Рис.
1.2. Установка надстройки
ПОИСК РЕШЕНИЯ Рис. 1.3. Добавление ограничения
Также следует установить ПАРАМЕТРЫ ПОИСКА РЕШЕНИЯ.
Нажимаем кнопку ПАРАМЕТРЫ (рис. 1.4) и в меню ПАРАМЕТРЫ
ПОИСКА РЕШЕНИЯ (рис. 1.5) устанавливаем метки «Линейная модель»,
«Автоматическое масштабирование» – ОК. Снова возвращаемся в меню ПОИСК РЕШЕНИЯ (рис. 1.4) и нажимаем кнопку ВЫПОЛНИТЬ.
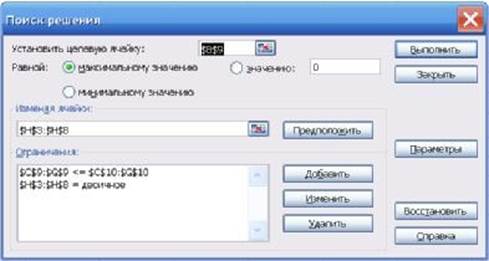
Рис. 1.4. Меню ПОИСК РЕШЕНИЯ
Если при составлении рабочей таблицы и вводе модели не было ошибок и задача имеет решение, то появится меню РЕЗУЛЬТАТЫ ПОИСКА
РЕШЕНИЯ (рис. 1.6). Нажимаем кнопку ОК и анализируем результаты (рис.
1.7).
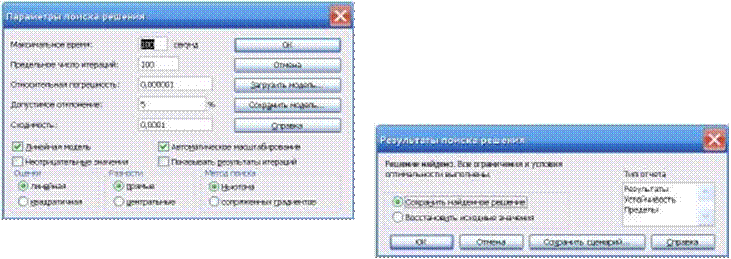 Рис.
1.5. Меню ПАРАМЕТРЫ
Рис.
1.5. Меню ПАРАМЕТРЫ
ПОИСКА РЕШЕНИЯ Рис. 1.6. Результаты поиска решения
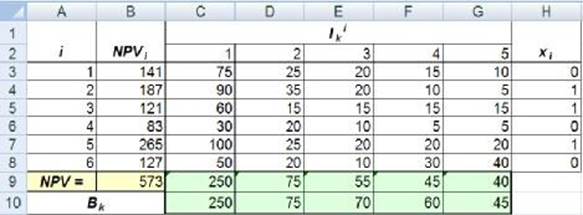
Рис. 1.7. Рабочая таблица с оптимальным решением
Таким образом, получаем, что при инвестировании 2-го, 3-го и 5-го проектов может быть получена максимальная суммарная чистая текущая стоимость в размере 573 д.е.
Пункт 2. Решение задачи при дополнительном условии.
Дополнительное условие рассматриваемого примера можно выразить посредством ограничения: x5 ≤ x4 или x5 − x4 ≤ 0. В отдельной ячейке, например, Н9, введем формулу, соответствующую, левой части данного ограничения: Н9 = Н7 – Н6. Далее вызываем ПОИСК РЕШЕНИЯ. Нажимаем кнопку ДОБАВИТЬ и вводим формулу H9 ≤ 0. Возвращаемся в меню ПОИСК РЕШЕНИЯ и нажимаем кнопку ВЫПОЛНИТЬ. Анализируем результаты поиска решения.
Пункт 3. Оформление отчета о проделанной работе.
План отчета.
1. Укажите фамилию, имя, название группы, номер варианта.
2. Запишите оптимизационную модель, по которой были произведены расчеты, с указанием экономического смысла переменных, целевой функции и ограничений.
3. Запишите оптимальное решение, которое было получено в 1-м пункте и дайте содержательный ответ на вопрос задачи.
4. Запишите оптимальное решение, полученное для ответа на дополнительный вопрос и проанализируйте его в сравнении с оптимальным решением, полученным ранее.
Лабораторная работа № 2
ЗАДАЧА ОПТИМАЛЬНОГО ФИНАНСИРОВАНИЯ ИНВЕСТИЦИОННОГО ПРОЕКТА
Постановка задачи.
Промышленная компания заключила контракт со строительной организацией о строительстве нового цеха. В условиях контракта сказано, что промышленная компания должна выплатить строительной организации 250 д.е. через два месяца, 250 д.е. через четыре месяца и 300 д.е. через шесть месяцев. Для финансирования этого проекта промышленная компания создает фонд. Причем промышленная компания вкладывает деньги в инвестиционный фонд только в начале первого месяца. При этом существует возможность вкладывать деньги в финансовые инструменты. Данные для финансовых инструментов заданы в таблице 2.1.
Таблица 2.1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.