Экономико-математические методы и модели в финансовой деятельности. Оптимальный инвестиционный проект, страница 39

9.  Изобразить портфели и комбинации, найденные в результате выполнения пунктов 4 – 8, а также безрисковый актив, в координатной плоскости (s ,_r). По соответствующим точкам построить участок эффективной границы множества инвестиционных возможностей портфелей, состоящих из акций заданных видов, и луч, являющийся эффективной границей множества инвестиционных возможностей комбинаций безрискового актива и акций заданных видов.

Методические указания по выполнению работы

Выборочные ожидаемые доходности акций заданных видов находятся по формуле:

1

                                                              r_i = n ∑kn=1 r_i^k ,                                        (7.1)

а стандартные отклонения доходностей:

                                                                                    1 n ( k            )2

                                                             s = ∑ r − r      ,                                      (7.2)

                                                                             i        n k=1    i            i

где n – число наблюдений.

Ковариационная матрица доходностей акций заданных видов имеет вид:

                                                                               s      s        s 

                                                      A = s 1121 s 1222 s 1323 .                                 (7.3)

s 31 s 32 s 33

где s _ij , i, j =1,3 – это ковариации доходностей акций видов i и j, т.е.

                                              s _ij = ¹n ∑kⁿ=1 (r_ik − r_i )⋅(r_jk − r_j ).                         (7.4)

Ожидаемая доходность портфеля находится по формуле:

r  _п = ∑ⁿ w_i r_i .          (7.5)

i=1

Дисперсию доходностей портфеля в матричном виде можно рассчитать по формуле (7.6).

                                                              D_п = w^Т ⋅ A⋅w,                                         (7.6)

где w – вектор-столбец долей w_i, i =1,3, w^Т – вектор-строка долей w_i, i =1,3, А – ковариационная матрица доходностей портфеля.

Тогда можно легко найти стандартное отклонение:

s  _п =      D_п       (7.7)

          Коэффициент “тета” портфеля находится по формуле:

r^п − r^f

                                                                    q_п =.                                               (7.8)

s _п

Задача максимизации ожидаемой доходности портфеля имеет вид:

r_п → max,

s _п ≤sˆ,

                                                           ^∑i₌ⁿ₁ wi =1,                                                     (7.9)

w_i ≥ 0, i =1,n.

Задача минимизации стандартного отклонения доходности портфеля:

s _п → max,

r_п ≥ rˆ,  ^ _n wi =1, (7.10) ∑

 i=1

w_i ≥ 0, i =1,n.

Задача оптимизации портфеля при наличии безрискового актива имеет вид:

q_п → max,

                                                              ∑ⁿ w_i =1,                                             (7.11)

i=1

w_i ≥ 0, i =1,n.

Порядок выполнения работы

Пункт 1. Расчет основных характеристик акций.

Введем в Excel таблицу исходных данных.

Для нахождения выборочных ожидаемых доходностей и стандартных отклонений доходностей акций воспользуемся встроенными функциями  СРЗНАЧ и СТАНДОТКЛОН. Введем эти функции в ячейки В15 и В16 соответственно и скопируем вправо (рис. 7.1).

 

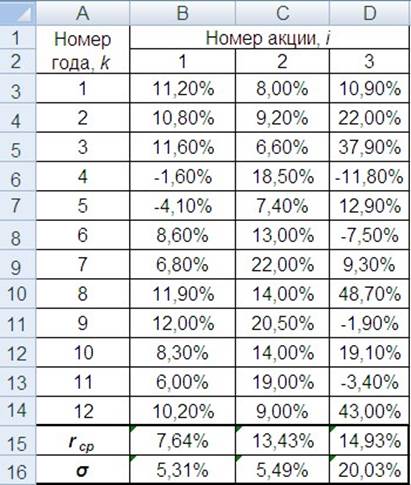
Рис. 7.1. Доходности акций и их характеристики

Пункт 2. Построение ковариационной матрицы.

Для построения ковариационной матрицы воспользуемся встроенной функцией КОВАР. В ячейке G3 введем соответствующую формулу, зафиксировав адреса ячеек с доходностями акций 1-го вида и скопируем эту формулу вправо до ячейки I3 (рис. 7.2). Аналогично рассчитаем 2-ю и 3-ю строку ковариационной матрицы.

 

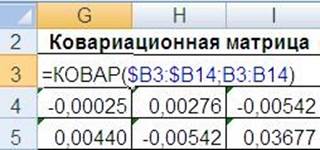
Рис. 7.2. Ковариационная матрица

Пункт 3.  

Введем в Excel необходимые формулы. Вначале создадим таблицу долей w_i, i =1,3 акций заданных видов в портфеле (в которой также введем формулу для нахождения суммы долей) (рис. 7.3).

Учитывая формулы (7.5) – (7.8) рассчитаем ожидаемую доходность, дисперсию, стандартное отклонение и значение «тета» портфеля. Для расчета ожидаемой доходности используем функцию СУММПРОИЗВ. Формула (7.6) может быть реализована в Excel с помощью встроенных функций МУМНОЖ и СУММПРОИЗВ. Напомним, что функция МУМНОЖ предполагает использование сочетания клавиш Ctrl + Shift + OK. Для поиска стандартного отклонения используем функцию КОРЕНЬ (рис. 7.3).

 

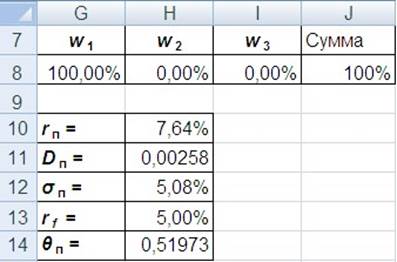
Рис. 7.3. Основные характеристики портфеля ценных бумаг

Пункт 4. Решение задачи максимизации ожидаемой доходности портфеля.