Экономико-математические методы и модели в финансовой деятельности. Оптимальный инвестиционный проект, страница 5

Решить задачу при дополнительном условии, что может быть принято только два из трех проектов под номером 2, 3, 4.

Вариант 12.

Решить задачу при дополнительном условии, что 3-й проект может быть принят только в случае принятия 1-го проекта.

Методические указания по выполнению работы

Предположим, что фирма может принять m инвестиционных проектов.

Для каждого из этих проектов известна чистая текущая стоимость NPV_i , i =1,m. Каждый из этих проектов требует инвестиций в течение n периодов времени. Обозначим через I_kⁱ размер инвестиций, требуемых для i-го проекта в k-том периоде. Для финансирования всех отобранных проектов фирма располагает в k-том периоде суммой B_k денежных единиц. Задача состоит в отборе проектов таким образом, чтобы суммарная  чистая текущая стоимость отобранных проектов была максимальна и при этом, чтобы в каждом периоде суммарные инвестиции, требуемые для финансирования отобранных проектов, не превышали выделенных сумм B_k . 

Для того, чтобы построить математическую модель этой задачи введем двоичные переменные  x_i, i =1,m. Положим x_i = 1 в случае, если i-й проект принимается, и x_i = 0 в случае, если i-й проект отвергается. Тогда суммарная текущая стоимость отобранных проектов будет равна ∑^m NPV_i ⋅ x_i , а

i=1

суммарные инвестиции, требуемые в k-том периоде для финансирования отобранных проектов – ∑^m I_kⁱ ⋅ x_i . 

i=1

Следовательно, математическая модель задачи имеет вид:

NPV ≡ ∑^m NPV_i ⋅ x_i → max ,                                        (1.1)

i=1

                                                               ^m                                                                                      B_k , k =1,n ,                                               (1.2)

i=1

x_i ∈{0,1}, i =1,m.                                                     (1.3)

В некоторых случаях налагаются дополнительные условия на процесс отбора проектов.   Например, 

•  если хотя бы один из двух проектов (с номерами i и j) должен быть принят, то к ограничениям задачи (1) – (3) добавляется условие: x_i + x _j ≥1;

•  если должно быть принято не более одного из двух проектов, то условие запишется в виде: x_i + x _j ≤1;

•  если проект j может быть принят только в случае принятия проекта i, то x _j ≤ x_i , и т.п.

Порядок выполнения работы

Пункт 0. Подготовительная работа.

Построим рабочую таблицу в Excel, содержащую исходные данные. В ячейках В3:В8 разместим значения чистых текущих стоимостей каждого проекта, С3:G8 – инвестиции для k-го проекта в i-том году, C10:G10 – имеющиеся денежные средства в k-ом году (рис. 1.1).

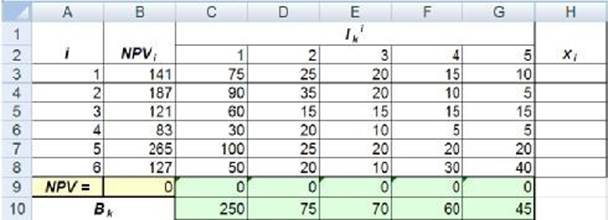
Рис. 1.1. Рабочая таблица

В ячейке В9 введем формулу для расчета суммарного значения NPV выбранных для инвестирования проектов: В9 = СУММПРОИЗВ(B3:B8; $H3:$H8). Знак $ выставляем для того, чтобы при копировании этой формулы в ячейки С9:G9 адреса ячеек H3:H8, отведенных под переменные, не изменялись. Функцию можно вывести при помощи команды ВСТАВКА – ФУНКЦИЯ – МАТЕМАТИЧЕСКИЕ – СУММПРОИЗВ или ввести вручную.