Экономико-математические методы и модели в финансовой деятельности. Оптимальный инвестиционный проект, страница 18

Найдем точку безубыточности для срока проекта, т.е. минимальное количество лет действия проекта, при котором чистая текущая стоимость проекта неотрицательна. Для этого будем уменьшать срок проекта до тех пор, пока NPV не станет отрицательной.

Уменьшим значение входного параметра n на единицу (с 7 до 6 лет). Также в формуле для расчета  NPV  уменьшим поле аргументов на одну ячейку: NPV = СУММ(DC₀ : DC₆). Если при n = 6 чистая текущая стоимость положительна, уменьшим срок проекта еще на один год (с 6 лет до 5 лет). При этом также в формуле для расчета  NPV  уменьшим поле аргументов на одну ячейку: NPV = СУММ(DC₀ : DC₅).

Пункт 4. Оценка вероятности событий с помощью имитационного моделирования.

По условию задачи относительные отклонения e_k , k =1,n подчиняются нормальному распределению с параметрами μ = 0 и σ = 10%. Введем эти значения в Excel в качестве входных параметров.

В Excel имеется датчик случайных чисел, распределенных равномерно на отрезке [0;1]: СЛЧИС().  Для того, чтобы с помощью этого датчика  получить нормально распределенные случайные числа нужно использовать функцию, обратную к функции нормального распределения. Такая функция в Excel’e имеет вид: НОРМОБР(y; m; s), где y – это вероятность, соответствующая нормальному распределению, а m и s – параметры нормального распределения. Подставив в НОРМОБР(y; m; s ) вместо y датчик равномерно распределенных случайных чисел СЛЧИС(), получим датчик случайных чисел, распределенных нормально с параметрами m и s:

НОРМОБР(СЛЧИС(); m; s ).

Формула Q_k = Q_k−1 ⋅(1+e_k ) реализуется в Excel следующим образом:

Q_k = Q_k−1 ⋅НОРМОБР(СЛЧИС();1;s )

Теперь в строке «Выпуск» генерируются случайные числа (рис. 3.6). 

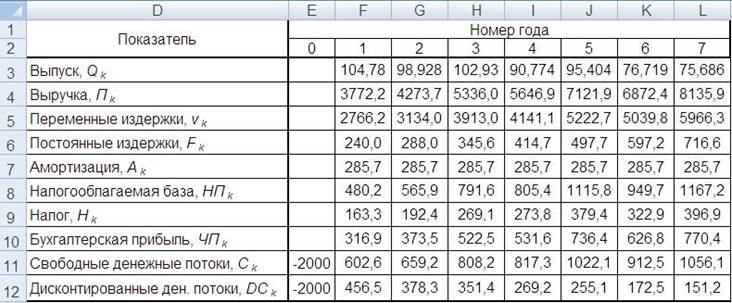
Рис. 3.6. Показатели инвестиционного проекта при нормально распределенном объеме выпуска по годам

При нажатии функциональной клавиши F9 совершается пересчет, т.е. генерируются новые случайные числа. 

Для того чтобы можно было найти выборочные характеристики выходных параметров, а также эмпирические вероятности, построим таблицу значений выходных параметров (NPV, IRR, IRR_real). Таблица будет содержать по 100 значений для каждого параметра.

Для этого вначале введем названия столбцов, номер первого значения, и адреса ячеек, в которых вычисляются соответствующие параметры (табл.

3.3).

Таблица 3.3

Затем заполним столбец номеров (от 1 до 100), выполнив следующие действия:

•  Поставим курсор в ячейку с номером 1;

•  Правка → Заполнить → Прогрессия^[4];

•  Расположение: по столбцам;

•  Тип: арифметическая;

•  Шаг: 1, предельное значение: 100;

•  ОК.

Чтобы заполнить построенную таблицу необходимыми значениями:

•  Выделим таблицу (без строки названий столбцов);

•  Данные → Таблица подстановки^[5];

•  Подставлять значения по строкам в: <введите адрес любой пустой ячейки>.

В результате таблица заполнится значениями. 

Для того чтобы можно было упорядочить числа по возрастанию, в таблице нужно заменить формулы значениями. Для этого, не снимая выделения, нужно сделать следующее^[6]:

•  Правка → Копировать;

•  Правка → Специальная вставка;

•  Вставить: значения;

•  Enter.

Теперь можно упорядочить значения таблицы по возрастанию, воспользовавшись сортировкой (рис. 3.7).

Найдем средние значения и выборочные стандартные отклонения выходных параметров при помощи статистических функций СРЗНАЧ и СТАНДОТКЛОН.

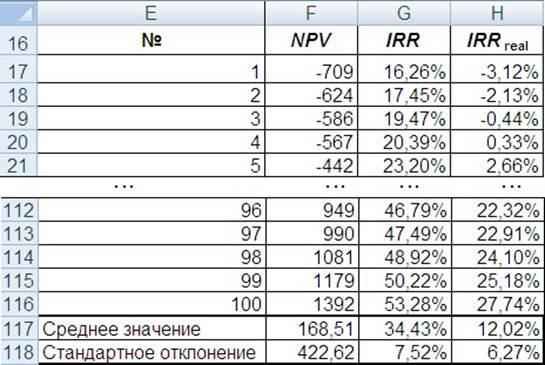
Рис. 3.7. Расчет статистических характеристик

Найдем эмпирическую (выборочную) вероятность того, что NPV < 0. В нашем примере 41 из 100 значений NPV оказались отрицательными, значит P(NPV < 0)= 0,41. Аналогично можно найти все остальные вероятности.

Пункт 5. Оформление отчета о проделанной работе.

План отчета.