Экономико-математические методы и модели в финансовой деятельности. Оптимальный инвестиционный проект, страница 13

Здесь через w_i^k обозначен вес вложений в финансовые инструменты вида i в k-м периоде. Причем будем считать, что w_i^k определяется по формуле

(2.4).

                                                                               w_i^k =     ^xi .                                                  (2.4)

∑x _j

t _j <k≤T_j

Приведем ограничение (2.3) к линейному виду. Подставив (2.4) в (2.3) после несложных алгебраических преобразований, получим соотношение

(2.5).

∑(R_i − R)⋅ x_i ≤ 0, k =1,n.                                        (2.5)

t_i <k≤T_i

Итак, математическая постановка задачи оптимального финансирования проекта следующая: минимизировать целевую функцию (2.1) при ограничениях (2.2), (2.5) и условии неотрицательности переменных x_i, i =1,m , т.е.

I₀ = ∑x_i → min

t_i =0

∑(1+ r_i )⋅ x_i − ∑x_i ≥ I_k , k =1,n,

                                                         T_i =k                              t_i =k

                                                           ∑( i            ) i                                                                 (2.6)

                                                                R − R ⋅ x ≤ 0, k =1,n,

t_i <k≤T_i

x_i ≥ 0, i =1,m.

Для удобства ввода модели в электронные таблицы Excel определим следующим образом коэффициенты a_i^k и b_i^k :

1+ r_i , если T_i = k; ai^k = ^−1, если t_i = k;

                                                                    _{0, если T}i ≠ _{k и t}i ≠ _k;                                      (2.7)

i =1,m. k = 0,n.

                                                             k      R_i − R, если t_i < k ≤ T_i ;

_bi _{= }

                                                                        0,                                             в противном случае;                                  (2.8)

i =1,m, k = 0,n.

С использованием формул (2.7), (2.8) задача (2.6) запишется в виде.

n

I x_i → min                                           (2.9)

i=1

∑ⁿ a_i^k ⋅ x_i ≥ I_k , k =1,n,                                          (2.10)

i=1

∑ⁿ b_i^k ⋅ x_i ≤ 0, k =1,n,                                           (2.11)

i=1

x_i ≥ 0, i =1,m.                                                    (2.12)

Порядок выполнения работы

Пункт 0. Подготовительная работа.

Сформируем таблицу и введем исходные данные для решения задачи (рис. 2.1). Ячейки F3:F14 отведем под переменные, в ячейке E16 запишем значение R , которое в нашем случае равно 5.

 

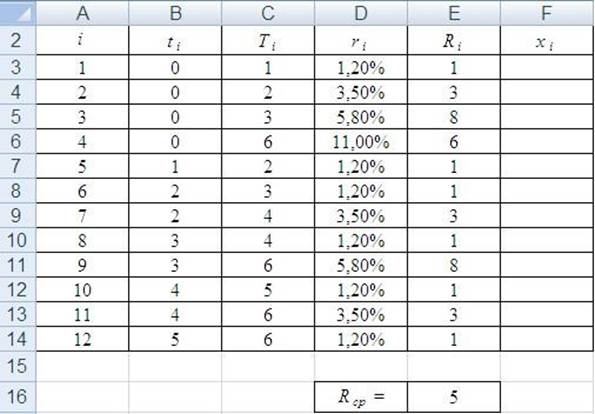
Рис. 2.1. Исходные данные

Для ввода в Excel целевой функции (2.9) и ограничений вида (2.10) сформируем таблицу (рис. 2.2). В ячейке I3 введем формулу, воспользовавшись логической функцией ЕСЛИ, имеющей формат ЕСЛИ (<логическое выражение>; <значение если истина>; <значение если ложь>). Затем введенную формулу скопируем вправо вниз до ячейки O14. При этом некоторые ячейки окажутся заполненными значениями «-1», что соответствует моменту вложения денег в финансовый инструмент, в некоторых появятся значения, соответствующие моменту получения денег и равные коэффициенту наращения, все остальные ячейки будут пустыми. В ячейках I15:O15 используем математическую функцию СУММПРОИЗВ. Ячейку I16 отведем под целевую функцию, в ней стоит выражение, противоположное выражению ячейки I15. В ячейки J16:O16 запишем денежные суммы, которые необходимо получить в конце каждого месяца.

 

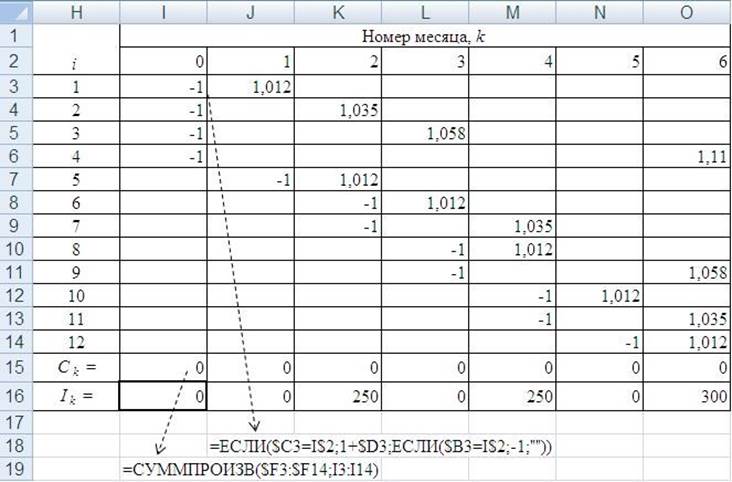
Рис. 2.2. Ввод формул для целевой функции и ограничений вида (2.10)

Осталось сформировать таблицу для ввода ограничений вида (2.11). В ячейки B20:G31 запишем формулы вида (2.8), используя логические функции ЕСЛИ и И(<логическое значение 1>; <логическое значение 2>;…). В ячейках B32:G32 используем функцию СУММПРОИЗВ (рис. 2.3).

 

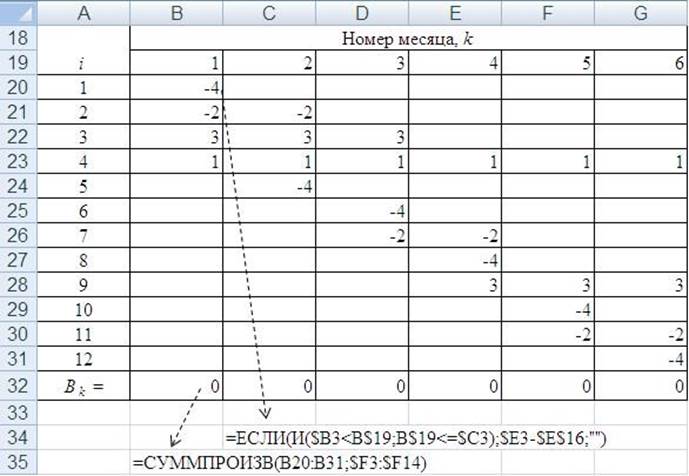
Рис. 2.3. Ввод формул для ограничений вида (2.11)

Пункт 1. Поиск оптимального решения.

Вызовем команду ПОИСК РЕШЕНИЯ из меню СЕРВИС (из закладки ДАННЫЕ для 2007 версии Excel) (рис. 2.4) и введем модель:

•  Установить целевую ячейку: I16;