Экономико-математические методы и модели в финансовой деятельности. Оптимальный инвестиционный проект, страница 20

Окончание таблицы 4.1

Вари- ант	Параметры						Номер года, i
			1	2	3	4	5	6	7	8	9	10
12	F = 150 s = 40 K = 115	Pi	72,5	73,9	74,3	84,6	90,6	99,6	102,3	109,5	111,3	113,6
		ti	1	1	2	2	3	3	3	4	4	4
		jкупi	5%	8%	9%	10%	12%	14%	15%	17%	18%	25%

Требуется:

1.  найти доходности к погашению облигаций;

2.  с помощью доходностей к погашению найти продолжительности облигаций;

3.  найти чистые доходности для первого, второго, третьего и четвертого годов;

4.  с помощью найденных чистых доходностей оценить рыночную стоимость четырехлетней s%-ной облигации с номинальной стоимостью K д.е. и купонным периодом 1 год.

Порядок выполнения работы

Пункт 0. Ввод исходных данных.

Построим таблицу исходных данных, используя числовые данные варианта 0 (рис. 4.1).

 

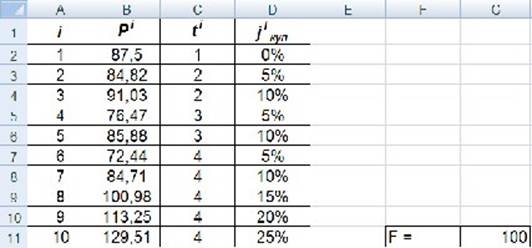
Рис. 4.1. Исходные данные

Пункт 1. Расчет доходности к погашению и продолжительности облигаций.

Построим таблицу денежных потоков облигаций (рис. 4.2).

 

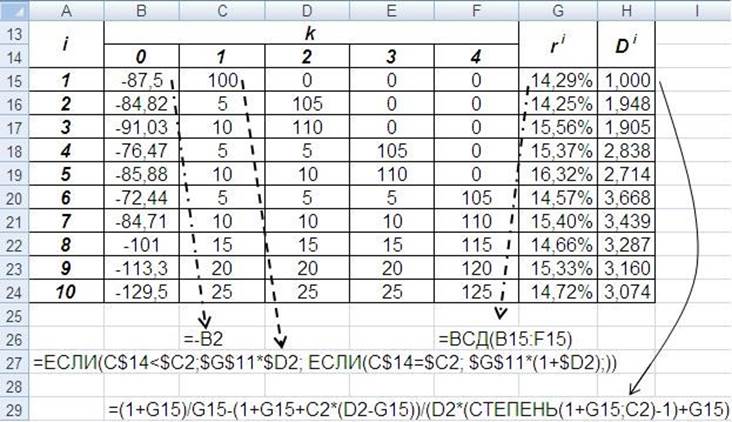
Рис. 4.2. Расчет доходности к погашению и продолжительности облигаций

В ячейках В15:В24 стоят значения = – Pⁱ, а в ячейках C15:F24 –  платежи C_kⁱ , которые вычисляются по формуле:

                                                                    F ⋅ j_купⁱ ,         если k < tⁱ

                                                              _kⁱ     ^            ⋅, если k = tⁱ                                       (4.1)

C  = F



                                                                   0,                 если k > tⁱ

Вводим формулу (4.1) в ячейку С15 и копируем по всей таблице. Доходности к погашению облигаций rⁱ найдем в этой же таблице с помощью встроенной функции ВСД.

Продолжительность облигаций найдем по формуле:

D 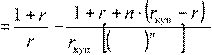 ⋅ 1+ r   −1 + r .       (4.2)

Пункт 2. Расчет чистых доходностей для каждого года.

Чистые доходности r_k находятся из системы уравнений (4.3):

                                                    ^∑kⁿ=1 (₁₊^C_r^kik )k = Pⁱ , i =1,m,                               (4.3)

либо вначале находятся коэффициенты дисконтирования d_k из системы уравнений:

                                                       ∑ⁿ C_kⁱd_k = Pⁱ, i =1,m,                                  (4.4)

k=1

а затем чистые доходности r_k находятся по формуле r_k =d_k^−1k −1.

Однако в случае, когда m>n эта система уравнений может не иметь точного решения. Тогда она решается приближенно. 

                                                     ∑ⁿ Ckidk = Pi +ei, i =1,m,                               (4.5)

k=1

При этом d_k подбираются таким образом, чтобы сумма ∑^m ( )e^{i 2} была

i=1

минимальна, и выполнялись условия: d_k ≤ d_k−1, k = 2,n , т.е. решается задача:

∑m ( )e^{i 2} → min

i=1 n    

                                                      eⁱ ,m,                                  (4.6)

k=1

d_k ≤d_k−1, k = 2,n, d_k ≥ 0, k =1,n.

Для того чтобы решить эту задачу в Excel, вначале создадим таблицу с коэффициентами дисконтирования d_k и чистыми доходностями r_k.

Начальные значения коэффициентов d_k можно взять равными 1.

 

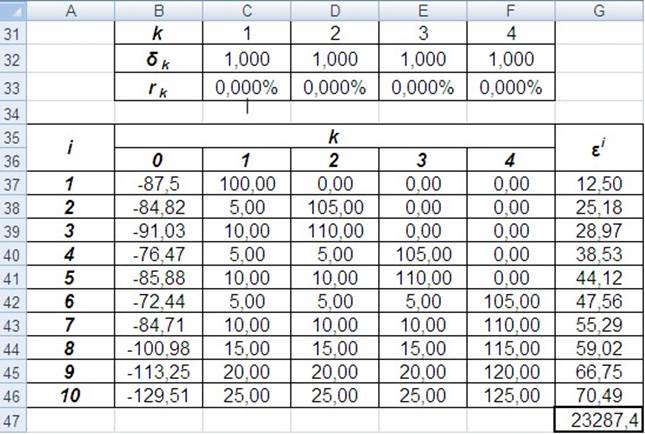
Рис. 4.3. Поиск чистых доходностей облигаций

Ячейки C32:F32, содержащие значения коэффициентов d_k – это изменяемые ячейки (т.е. переменные) задачи (4.6).

Затем создадим таблицу (рис. 4.3), в которой рассчитаем дисконтированные денежные потоки DC_kⁱ по формуле DC_kⁱ = C_kⁱd_k (ячейки