Другие предметы \ Финансовый анализ

Экономико-математические методы и модели в финансовой деятельности. Оптимальный инвестиционный проект, страница 21

C37:F46). Также найдем погрешности ei по формуле ei = ∑n DCki с помощью

k=0

встроенной функции СУММ (ячейки G37:G46). В ячейке G47 найдем целевую функцию модели (4.6) с помощью встроенной функции СУММКВ. 

Теперь мы можем решить задачу (4.6) с помощью модуля «Поиск решения». Вызываем меню СЕРВИС – ПОИСК РЕШЕНИЯ (для Excel 2007:

ДАННЫЕ – ПОИСК РЕШЕНИЯ).

Установить целевую ячейку G47 равной минимальному значению. Изменяя ячейки С32:F32. Ограничения ДОБАВИТЬ. В меню «Добавление ограничения» (рис. 4.4) вводим соответствующую формулу. Нажимаем кнопку ОК. Далее устанавливаем ПАРАМЕТРЫ поиска решения:

Неотрицательные значения. Нажимаем кнопку ВЫПОЛНИТЬ (рис. 4.5) и анализируем полученное оптимальное решение.

 

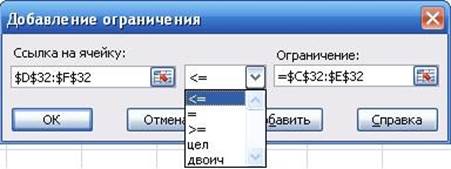
Рис. 4.4. Меню «Добавление ограничения»

 

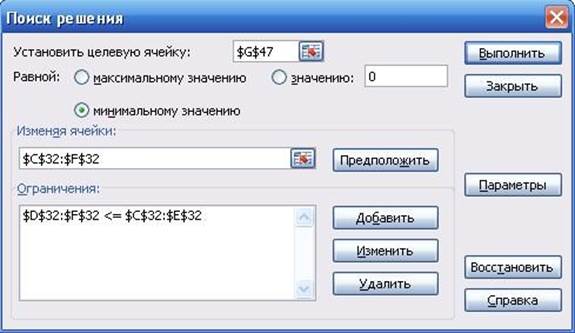
Рис. 4.5. Меню «Поиск решения»

Пункт 3. Составление отчета о проделанной работе.

План отчета:

1.  Запишите фамилию, имя, название группы, номер варианта.

2.  Чему равны доходности к погашению облигаций? Что они означают?

3.  Запишите значения продолжительностей облигаций? Каков их смысл?

4.  Чему оказались равны чистые доходности для каждого года?

5.  Дайте ответ на 4-й вопрос задачи.

Лабораторная работа № 5

ОЦЕНКА РИСКА ЗАЁМЩИКА С ИСПОЛЬЗОВАНИЕМ МЕТОДОВ РЕГРЕССИОННОГО И ДИСКРИМИНАНТНОГО АНАЛИЗА

Постановка задачи.

Известна следующая информация по кредитам:

•  имел ли место дефолт для данного кредита (если да, то z = 1, если нет, то z = 0);

•  отношение активов к оборотному капиталу заемщика x1;

•  отношение обязательств к собственному капиталу x2;

•  отношение активов к прибыли x3.

Финансовые коэффициенты x1, x2 и x3 потенциального заемщика равны x10 = 2,07, x20 =1,36 и x30 =14,3 соответственно.

Информация по кредитам приведена в таблице 5.1. Варианты заданий – в таблице 5.2.

Таблица 5.1

Номер наблюдения

Информация о дефолте, z

Финансовые коэффициенты

x1

x2

x3

1

1

3,40

0,61

16,2

2

0

2,38

1,38

4,5

3

1

3,44

0,78

15,3

4

1

2,07

1,84

9,9

5

0

3,76

0,37

7,2

6

1

2,41

1,17

16,2

7

1

2,80

1,12

16,2

8

0

2,63

0,72

17,1

9

0

3,10

0,80

8,1

10

1

3,82

0,71

11,7

11

0

2,85

0,48

18,9

12

1

4,11

0,39

10,8

13

0

3,31

0,69

9,0

14

0

3,06

0,57

12,6

15

1

3,24

0,73

18,0

16

0

2,78

0,82

13,5

17

1

3,69

0,41

18,9

Требуется:

1.  построить линейную регрессионную модель для оценки кредитного риска и с ее помощью оценить вероятность дефолта для потенциального заемщика;

2.  построить регрессионную дискриминантную модель, найти граничное значение zгр и отнести потенциального заемщика к группе с высоким либо низким кредитным риском.

Таблица 5.2

Скачать файл