Экономико-математические методы и модели в финансовой деятельности. Оптимальный инвестиционный проект, страница 16

Предположим, что амортизация – линейная, причем инфляция не учитывается. Тогда амортизация в k-том году:

                                                         A_k = ^I0 .                                             (3.5)

n

Налогооблагаемая база в k-том году:

                                                   НП_k = Пр_k − A_k .                                       (3.6)

Предположим, что налог взимается только в том случае, когда налогооблагаемая база положительна. Тогда налог за k-й год:

                                                H_k = max(НП_k ;0)⋅t .                                    (3.7)

Бухгалтерская прибыль в k-том году  после уплаты налога:

                                                  ЧП_k = НП_k − H_k .                                       (3.8)

Заметим, что амортизация – это фиктивный денежный поток. (Поскольку начальные инвестиции происходят в начальный момент времени.) Следовательно, свободный денежный поток C_k за k-й год определяется следующим образом:

                                                    C_k =ЧП_k + A_k .                                         (3.9)

Формулы (3.1) – (3.9) позволяют однозначно определить свободный денежный поток C_k в k-том году с помощью значений входных параметров  I₀, Q, p, v, F, n, t, i. Следовательно, выходной параметр C_k можно рассматривать как функцию от перечисленных выше входных параметров, т.е.

                                              C_k = C_k (I₀,Q, p,v,F,n,t,i).                                (3.10)

Для того, чтобы найти чистую текущую стоимость проекта, найдем вначале номинальную внутреннюю доходность альтернативных проектов r по формуле:

                                                    r = rˆ + i + rˆ⋅i,                                      (3.11)

где rˆ – реальная внутренняя доходность альтернативных проектов, i – уровень инфляции. 

Теперь можно найти чистуютекущую стоимость проекта:

                                                  NPV n C                                                             k       (3.12)

Из (3.10) – (3.12) следует, что

                                         NPV = NPV(I₀,Q, p,v,F,n,t,i,r^ˆ).                           (3.13)

Номинальную внутреннюю доходность данного проекта IRR можно найти, решив следующее уравнение:

                                               ∑kn=1 (1+CIRRk )k = I0                                  (3.14)

Из (3.10) и (3.14) следует, что 

                                            IRR = IRR(I₀,Q, p,v,F,n,t,i).                              (3.15)

С помощью номинальной внутренней доходности проекта можно найти его реальную доходность по формуле:

                                              IRRreal = IRR −i .                                (3.16)

1+ i Из (3.15) и (3.16) следует, что

                                                  IRR_real = IRR_real(I₀,Q, p,v,F,n,t,i).                           (3.17)

Порядок выполнения работы

Пункт 0. Подготовительная работа.

Bведем в Excel значения входных параметров, соответствующих варианту 0 (рис. 3.1).

В ячейке В12 введем формулу (3.11) для определения номинальной внутренней доходности альтернативных проектов (которая будет использоваться в качестве ставки дисконтирования свободных денежных потоков проекта).

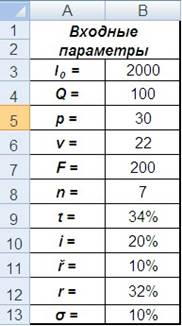
Рис. 3.1. Исходные данные

Пункт 1. Расчет основных параметров.

Построим таблицу для нахождения денежных потоков проекта. Введем соответствующие формулы для расчета показателей 1-го года (табл. 3.2). Здесь придется использовать встроенные функции СТЕПЕНЬ, МАКС. Во всех формулах должны фигурировать ссылки на ячейки с ранее введенными исходными данными задачи. Затем скопируем эти формулы вправо вплоть до 7-го года. Для начального момента времени понадобятся формулы только для значений свободных и дисконтированных денежных потоков проекта, что соответствует начальным инвестициям.

Таблица 3.2