Анализ мировых тенденций в проектировании современных бензиновых двигателей, страница 18

- силу, направленную вдоль оси шатуна, сжимающую или растягивающую его в зависимости от знака силы

P_ш можно разложить на:

- касательную силу

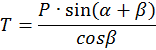
- радиальную силу

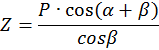
Угол β определяется из условия

Крутящий момент, действующий на КШМ одного цилиндра:

3.4 Выбор схемы заклинки кривошипов, порядка работы цилиндров и уравновешивание двигателя.

При нечетном числе цилиндров в блоке схема коленчатого валаможет быть только равномерной продольно – нессиметричной, не зависимо от тактности двигателя. Выбранная компоновочнаяй схема – число цилиндров i=5,  двигатель одноблочный  (5 цилиндров в ряд).  Из условия обеспечения равенства между вспышками в цилиндрах двигателя углы между кривошипами и вспышками в двигателе:

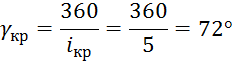
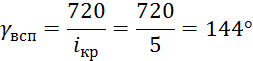
Заклинку кривошипов двигателя выбираем из условия наиболее благоприятного чередования вспышек в цилиндрах двигателя. Направление вращения вала, если наблюдать двигатель со стороны, противоположной отбору мощности, по часовой стрелке. Порядок работы цилиндров по блоку при выбранной схеме расположения кривошипов вала и известном направлении его вращения определяется по мере проворачивания схемы кривошипов вокруг оси коленчатого вала. При этом вспышки назначаются с приходом кривошипов в  В.М.Т. цилиндров блока. Назначим следующий порядок работы цилиндров двигателя:

Вспышки в цилиндрах двигателя происходят через равные интервалы (144°), вследствие чего выходной крутящий момент оказывается равномерным. График выходного крутящего момента представлен на рисунке 32.

Уравновешивание двигателя рассматривается только с учётом воздействия сил инерции возвратно-поступательно движущихся и вращающихся неуравновешенных масс (ПДМ и ВНМ) и продольных моментов этих сил, действующих в плоскостях, проходящих через ось коленчатого вала.

Для анализа динамических свойств выбранной схемы строим векторные диаграммы сил P_R, C_I, C_II (рис. 27).

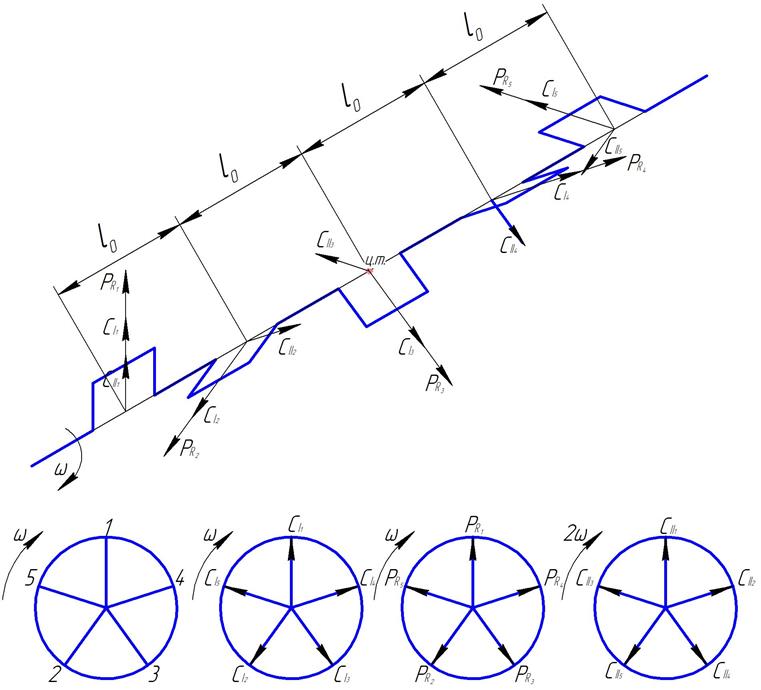
Рисунок 27 Схема заклинки кривошипов коленчатого вала и направление действия сил, действующих в КШМ..

Все диаграммы имеют схему пятиконечной звезды, следовательно, векторные многоугольники всех сил по форме будут одинаковы. На рисунке 28 показан векторный многоугольник сил C_I. Векторный многоугольник замкнут, следовательно, результирующий вектор равен нулю и сумма сил равна нулю, т.е.

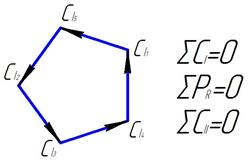
Рисунок 28 Векторный многоугольник сил C_I

Каждая неуравновешенная вращающаяся масса m_R развивает центробежную силу

P_R = m_R × R × w², радиус-вектор которой направлен по радиусу соответственного кривошипа и вращается вместе с ним вокруг оси коленчатого вала с угловой скоростью  w в плоскости осей цилиндров рассматриваемого отсека двигателя.

Каждая поступательно движущаяся масса развивает действующую вдоль оси соответственного цилиндра силу инерции, которая может быть определена в виде двух составляющих сил инерции первого и второго порядков:

где P_I – силы инерции первого порядка;

P_II – силы инерции второго порядка.

Шесть условий полной динамической самоуравновешенности двигателя – равенство нулю результирующих сил инерции и продольных моментов от этих сил:

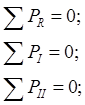
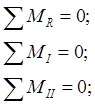
Выбрав полюс в центре вала (на пересечении оси третьего цилиндра с осью коленчатого вала), определяем величину действующих моментов:

Откладывая в масштабе векторы этих моментов с учетом их направления, находим результирующие векторы моментов (рис. 29).

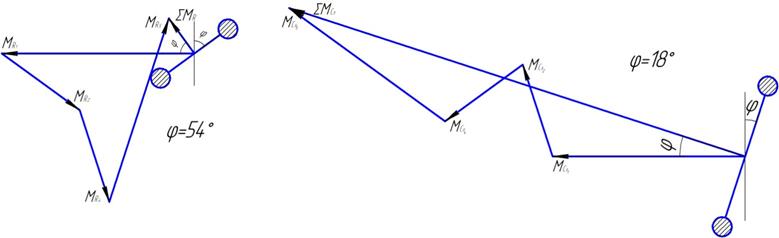
Рисунок 29 Результирующие векторы моментов

Величина и направление результирующего вектора находится изрешения многоугольника или непосредственным измерением. Измерив его и умножив на масштаб определяем велечину неуравновешенного результирущего момента. В данном случае величина неуравновешенного результирующего момента и угол, который составляет плоскость действия этого момента с плоскостью осей цилиндров, соответственно равны:

Реально действующие неуравновешенные моменты первого и второго порядка равны:

где m_R – массы, совершающие вращательные движения вокруг оси коленчатого вала с постоянной скоростью ω (НВМ);