Методическое пособие для выполнения лабораторных работ по темам: Механика. Колебания и волны. Молекулярная физика, термодинамика, явления переноса, страница 9

          Если колебания совершаются при наличии сил сопротивления, то энергия системы частично затрачивается на их преодоление. Вследствие этого амплитуда колебаний постепенно уменьшается, т.е. колебания будут затухающими.

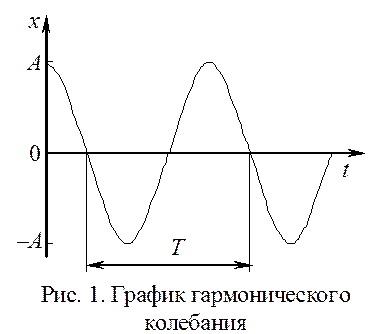Таким образом, затухающие колебания совершаются при наличии двух сил: силы, возвращающей систему в положение равновесия, и силы сопротивления среды. При малых скоростях сила сопротивления прямо пропорциональна скорости υ:

F_сопр = –rυ,                     (6)

где r – коэффициент сопротивления среды. Знак минус показывает, что сила сопротивления направлена в сторону, противоположную скорости.

          Для затухающих колебаний второй закон Ньютона имеет вид:

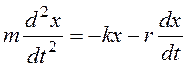                                      .                                                (7)

Решением уравнения (7) является выражение:

x = A₀e^–dtcos(wt + α),                                              (8)

где A₀ – начальная амплитуда колебаний; d– коэффициент затухания, равный

d = ;                                                                 (9)

w – циклическая частота затухающих колебаний, равная w = ; w₀ – собственная частота колебаний системы. Собственной частотой колебаний называется частота колебаний в отсутствие сил сопротивления среды. Смещение колеблющейся системы в начальный момент времени равно
x₀ = A₀cosα.

          Из уравнения (8) видно, что амплитуда затухающих колебаний уменьшается с течением времени по экспоненциальному закону:

A = A₀e^–dt.                                                     (10)

График затухающего колебания представлен на рис. 2.

Кроме перечисленных выше величин A₀, d, w, затухающие колебания характеризуются также логарифмическим декрементом D. Логарифмический декремент колебаний – безразмерная величина, равная натуральному логарифму отношения двух амплитуд, отстоящих друг от друга на время, равное одному периоду

D = 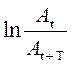                                                      (11)

Из формулы (11) следует, что логарифмический декремент – величина, обратная числу колебаний N_e, за которое амплитуда уменьшается в е раз. Для характеристики колебательной системы также используется величина, называемая добротностью Q. При малых значениях логарифмического декремента (D << 1) добротность колебательной системы равна                                                                                         Q ,

тогда

Q = pN_e.

Подставив в уравнение (11) A_t = A₀e^–dt   и A_{t + T} = A₀e^{–d(t + T)}, получим связь между параметрами затухающего колебания – логарифмическим декрементом, коэффициентом затухания и периодом колебаний:

D = dТ.                                                         (12)

          Для определения логарифмического декремента нужно измерить амплитуды двух последовательных колебаний и взять натуральный логарифм их отношения. На опыте измеряют амплитуду в начальный момент времени A₀ и амплитуду A_t через N полных колебаний.

          Получим формулу для вычисления логарифмического декремента. Выразим отношение двух амплитуд:

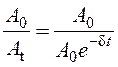 = e^δt.

Так как t = NT, где N – число полных колебаний, Т – период колебаний, то 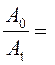                                                                     e^δNT.

Используя соотношение (12), получим

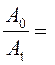e^DN.

Найдем натуральный логарифм отношения амплитуд:

ln = lne^DN = DN,

откуда

D = 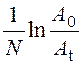.                                               (13)

Описание установки

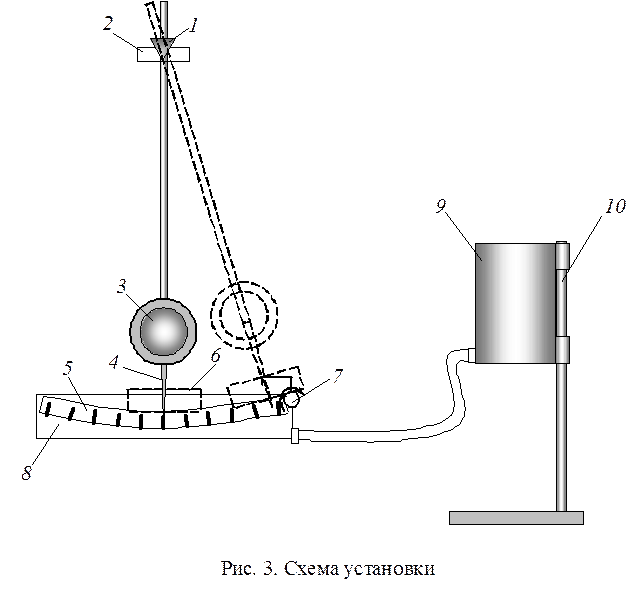
          На рис. 3 изображена установка для наблюдения затухающих колебаний. Массивный маятник с длиной стержня около двух метров подвешен на треугольном стальном ноже 1, опирающемся на кронштейн 2. На стержне укреплен массивный диск 3. На нижнем конце стержня укреплен указатель 4 для отсчета числа делений по шкале 5. На стержне также закреплена лопатка 6. Маятник удерживается в отклоненном положении с помощью механического фиксатора 7. При повороте фиксатора маятник приходит в колебательное движение.

          В работе изучаются затухающие колебания в воздухе и в воде. Чтобы заполнить кювету 8 водой, емкость 9 фиксируется в верхнем положении на кронштейне 10, и вода самотеком наливается в кювету через шланг.

Порядок выполнения работы

1.  Установить маятник в крайнее правое положение с помощью фиксатора 7. Определить начальное значение амплитуды A₀ по шкале и записать его.

2.  Освободить маятник, повернув фиксатор, и одновременно включить секундомер. Вести отсчет числа колебаний маятника и через каждые 50 колебаний отмечать по шкале значение амплитуды колебаний А_t.

3.  Через 250 колебаний остановить секундомер и записать его показание.

4.  Наполнить сосуд водой и повторить опыт. Вести отсчет амплитуды через каждые 25 колебаний. Записать время 125 колебаний. В случае быстрого затухания амплитуду измерять чаще, например, через каждые 10 колебаний.

5.  По формуле (13) рассчитать логарифмический декремент колебаний в воздухе и в воде.

6.  Обработать результаты по методу Стьюдента. Записать приближенное значение логарифмического декремента колебаний в воздухе и в воде с указанием абсолютной и относительной погрешности.

7.  По результатам измерений на одном графике построить зависимости амплитуды от времени для затухающих колебаний в воздухе и в воде.

8.  Вычислить период колебаний маятника в воздухе и в воде.

9.  Используя формулу (12) рассчитать коэффициент затухания колебаний маятника в воздухе и в воде.

10.  Записать уравнения затухающих колебаний в виде (8), подставив в него полученные в работе величины A₀, d, w и a.

11.  Используя формулу (9), рассчитать коэффициент сопротивления среды (воздуха и воды).

12.  Сделать выводы по работе.

Таблица

Результаты измерений и вычислений

№ п/п	В воздухе				В воде
	А0	Аt	N	D	А0	Аt	N	D
1			50				25
2			100				50
3			150				75
4			200				100
5			250				125
Среднее значение D					Среднее значение D
Абсолютная погрешность DD					Абсолютная погрешность DD