Методическое пособие для выполнения лабораторных работ по темам: Механика. Колебания и волны. Молекулярная физика, термодинамика, явления переноса, страница 11

Расстояние между двумя смежными узлами или пучностями называется длиной стоячей волны. Следовательно, длина стоячей волны равна половине длины бегущей волны:

l_ст = .                                                           (11)

Построим график стоячей волны. По уравнению (5) рассчитаем смещения x для фиксированных моментов времени t = 0, T/8, T/4, 3T/8, T/2. В каждое из получившихся уравнений x = f(x) подставим координаты x = 0, l/4, l/2, 3l/4, l, 5l/4… . Результаты расчетов приведены ниже.

Полученные зависимости x = f(x) изображены на рис. 1 и представляют собой своего рода «мгновенные фотографии» стоячей волны.

Стоячая волна имеет следующие особенности:

1)  амплитуда колебаний частиц различна в разных местах среды;

2)  в пределах участка среды от одного узла до другого все частицы колеблются в одной фазе, при переходе через узел фаза колебаний меняется на противоположную;

3)  в отличие от бегущей волны она не переносит энергию.

t = 0,   x = 2Acosx
x	0	l/4	l/2	3l/4	l	5l/4
x	2A	0	–2A	0	2A	0
t = ,   x = 2Acosxcos, x = Acosx
x	0	l/4	l/2	3l/4	l	5l/4
x	A	0	–A	0	A	0
t = ,   x = 2Acosxcos, x = 0
x	0	l/4	l/2	3l/4	l	5l/4
x	0	0	0	0	0	0
t = ,   x = 2Acosxcos, x = –Acosx
x	0	l/4	l/2	3l/4	l	5l/4
x	–A	0	A	0	–A	0
t = ,   x = 2Acosxcos, x = –2Acosx
x	0	l/4	l/2	3l/4	l	5l/4
x	–2A	0	2A	0	–2A	0

Получим формулу для расчета скорости звука в данной работе. Скорость волны связана с длиной бегущей волны λ и с частотой ν соотношением

υ = λν.                                                 (12)

Из формулы (11) следует, что λ = 2λ_ст, тогда

                                                           υ = 2λ_стν.                                            (13)

По формуле (13) можно рассчитать скорость звука при температуре эксперимента.

Зависимость скорости звука от температуры описывается соотношением

                                                 υ = υ₀,                                               (14)

где υ₀ – скорость звука при 0 ºС, t – температура в ºС, α – температурный коэффициент объемного расширения газа. Для воздуха α = (3,67 ± 0,05)·10^–3 ºС^–1. Из формулы (14) выразим скорость звука при 0 ºС:

                                                 υ₀ = 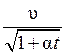.                                                            (15)

Подставив (13) в (15), получим расчетную формулу:

                                           υ₀ = 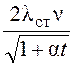.                                                (16)

Упрощенное описание установки и процессов, в ней происходящих

          Установка для определения скорости звука (рис. 2) состоит из резонатора 1, звукового генератора 2, осциллографа 3 и отсчетной линейки 4. Резонатор представляет собой закрытую с обоих торцов трубу, в которую вмонтирован телефон 5 и подвижный шток 6 с микрофоном 7. Звуковой генератор создает электрические колебания определенной частоты. Телефон преобразует эти колебания в звуковые колебания той же частоты. Звуковая волна от телефона распространяется внутри резонатора. В результате интерференции прямой и отраженной звуковой волны в резонаторе возникает стоячая волна, которая представляет собой чередующиеся сгущения и разрежения воздуха.

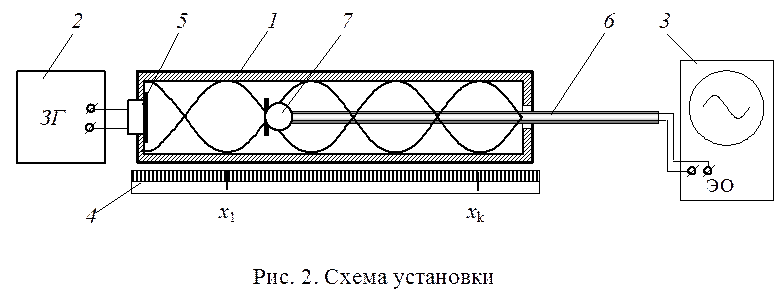
          На рис. 2 условно изображена стоячая волна, пучностям которой соответствует наибольшая амплитуда. Звук улавливается микрофоном и преобразуется в электрический сигнал, подаваемый на осциллограф. На экране осциллографа наблюдается сигнал синусоидальной формы, амплитуда которого пропорциональна амплитуде звуковых колебаний в данном месте резонатора. Когда мембрана микрофона находится в пучностях стоячей волны, амплитуда воспринимаемых колебаний максимальна, а когда в узлах – минимальна.

          На опыте обычно измеряют положение первого максимума x₁ и последнего максимума x_k и рассчитывают длину стоячей волны по формуле

                                                 λ_ст = 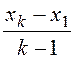,                                               (17)

где k – число максимумов.

          В несколько более точном представлении схема эксперимента и происходящие в ней явления выглядит иначе. Диаметр микрофона равен внутреннему диаметру резонатора. Таким образом, между микрофоном и телефоном существует замкнутое пространство, в котором распространяются падающая и отраженная волны. Стоячие волны возникают в том случае, когда между мембранами телефона  микрофона укладывается целое число длин волн λ_ст и возникает явление резонанса, отчетливо воспринимаемое на слух и регистрируемое осциллографом.

Порядок выполнения работы

1.  Включить звуковой генератор и установить частоту колебаний по указанию преподавателя (рекомендуемые частоты 900, 1000, 1100 Гц).

2.  Перемещая шток с микрофоном по направлению от источника колебаний, определить число максимумов k с помощью осциллографа. По отсчетной линейке найти положение первого максимума x₁ и последнего максимума x_k. Результаты измерений занести в таблицу.

Таблица

Результаты измерений и вычислений

№ п/п	n, Гц	k	x1	xk	lст	υ0, м/с

3.  Для каждого значения частоты выполнить не менее трех измерений. При этом каждый раз рекомендуется заново устанавливать частоту на звуковом генераторе.

4.  По формуле (17) рассчитать длину стоячей волны, а по формуле (16) – скорость звука в воздухе при 0 ºС. Результаты вычислений записать в таблицу.