Приборы и принадлежности: сосуд с капилляром, секундомер, мерный и химический стаканы, барометр.
Теоретическое введение
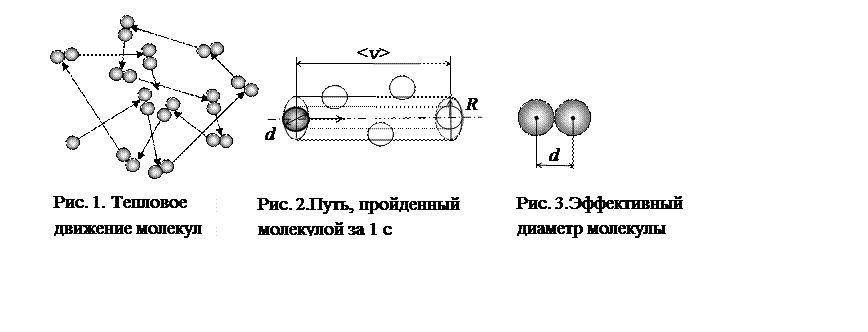
Молекулы газа, находясь в тепловом
движении, непрерывно сталкиваются друг с другом (см. рис. 1). При нормальных
условиях каждая молекула воздуха за одну секунду испытывает до 109
столкновений с другими молекулами (для упрощения
задачи не будем принимать во внимание химический состав воздуха, а будем
рассматривать некую эффективную молекулу). Под столкновением молекул
подразумевают процесс взаимодействия между молекулами, в результате которого
молекула изменяет направление своего движения.
Расстояние, проходимое молекулой между двумя последовательными столкновениями, называется длиной свободного пробега l.
Длина свободного пробега между отдельными столкновениями молекулы могут значительно отличаться друг от друга, поэтому вводят понятие средней длины свободного пробега <l>, которая определяется как отношение:
, (1)
где <v> и <z> – средняя скорость и среднее число столкновений молекулы в единицу времени.
Весьма приближенно число столкновений молекул за одну секунду можно подсчитать исходя из следующих соображений. Условно изобразим путь, пройденный молекулой за 1 с, прямой линией (рис. 2), длина которой численно равна <v>. Пусть в окружающем пространстве в единице объема содержится n молекул. Тогда рассматриваемая молекула, двигаясь по прямой, столкнется со всеми молекулами, центры которых лежат внутри цилиндра радиусом R, равным эффективному диаметру молекул d. Под эффективным диаметром понимается минимальное расстояние (рис. 3), на которое сближаются при столкновении центры двух молекул.
Так как объем цилиндра равен pR2<v> = pd2<v>, то всего молекул в нем окажется pd2<v>n. С этими молекулами и произойдут столкновения за 1 с. Таким образом, <z> = pd2<v>n.
Более точный расчет с учетом распределения Максвелла молекул по скоростям приводит к выражению:
. (2)
Подставив это значение <z> в (1) получим для средней длины свободного пробега следующую формулу:
. (3)
После замены pd2 на эффективное сечение молекулы s, формула (3) принимает вид:
. (4)
При постоянной температуре концентрация n пропорциональна давлению p (n = p/kT). Следовательно, средняя длина свободного пробега обратно пропорциональна давлению:
. (5)
Эффективное сечение молекул уменьшается с повышением температуры по уравнению
(6)
где – s0 величина, которую можно рассматривать как истинный диаметр молекулы, С – константа.
В соответствии с уравнением (6) при повышении температуры длина свободного пробега увеличивается. При нормальных условиях средняя длина свободного пробега молекул в газе составляет величину порядка 10–7 м. При очень высоком вакууме соударений молекул между собой практически не происходит. Они ударяются только о стенки сосуда и длина пробега молекулы становится постоянной, равной линейным размерам сосуда.
Столкновения молекул, происходящие в газах в результате теплового движения молекул, определяют характер процессов, известных под названием явлений переноса. К этим процессам относятся диффузия, теплопроводность и внутреннее трение или вязкость.
Диффузией называется самопроизвольный процесс, возникающий при наличии градиента концентрации в системе, заключающийся в переносе массы в направлении убывания концентрации и совершающийся за счет теплового движения атомов, молекул, ионов, или более крупных агрегированных частиц. Диффундировать могут как растворенные в веществе посторонние частицы, так и частицы самого вещества (самодиффузия).
Теплопроводность – это процесс переноса теплоты внутри неравномерно нагретой среды ппри наличии градиента температуры и при условии, что конвекция и другие явления устранены. При этом молекулы, находящиеся в более нагретых областях и обладающие в среднем более высокой кинетической энергией, при хаотическом тепловом движении переносят энергию в более холодные области, в результате чего происходит выравнивание температуры по всей области.
Внутреннее трение или вязкость – это свойство жидкостей и газов оказывать сопротивление перемещению одной их части относительно другой. При переходе частиц (атомов, молекул, ионов) из одного слоя в другой, движущихся относительно друг друга с некоторой скоростью, они переносят с собой импульс, при этом слой, движущийся быстрее, замедляется, а слой, движущийся медленнее, ускоряется.
Все явления переноса формально могут быть описаны уравнением:
, (7)
где J – поток переносимой величины (массы, теплоты, импульса), k – коэффициент пропорциональности (диффузии D, теплопроводности k, внутреннего трения h), dJ/dn – градиент переносимой величины (концентрации, температуры, скорости) вдоль нормали к площадке DS, через которую осуществляется перенос величины J, t – время.
Молекулярно-кинетическая теория газов позволяет во всех деталях интерпретировать явления переноса и установить связь между коэффициентами переноса (диффузии, теплопроводности, вязкости):
(8)
, (9)
, (10)
где r – плотность вещества, СV – удельная теплоемкость газа при постоянном объеме.
Последнее уравнение положено в основу определения средней длины свободного пробега молекул воздуха в данной работе.
Из формулы (9) получаем:
(10)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.