Методическое пособие для выполнения лабораторных работ по темам: Механика. Колебания и волны. Молекулярная физика, термодинамика, явления переноса, страница 7

          Таблица 2

Измерения периода колебаний оборотного маятника при положении чечевицы А₂ , равном b_x = . . .  см   

Контрольные вопросы

1. Что такое математический маятник? Что такое физический маятник?

2. Запишите формулы для периодов колебаний математического и физического маятников. Какие предположения использованы при выводе этих формул?

3. Что называется приведенной длиной физического маятника?

4. Докажите справедливость утверждения: «Приведенная длина физического маятника всегда больше расстояния между точкой подвеса и центром масс маятника».

5. Что называется центром качания физического маятника?

6. Докажите справедливость утверждения: «Маятник, подвешенный в центре качания О', имеет такую же приведенную длину, какую он имел, когда был подвешен в исходной точке О».

7. Какой маятник называют оборотным? Как в данной работе с помощью оборотного маятника определяют величину ускорения свободного падения?

8. Тонкий однородный абсолютно твердый стержень, имеющий массу m и длину r, подвешен за один из своих краев. Найдите положение центра качания, соответствующего этой точке подвеса.

9. Физический маятник представляет собой однородное тело, обладающее центром симметрии. Докажите равенство периодов колебаний этого маятника для любых двух точек подвеса, равноотстоящих от центра масс и лежащих на прямой линии, проходящей через центр масс. Докажите, что эти две точки не обладают свойством взаимности. Имеется ли центр симметрии у физического маятника, использованного в настоящей работе?

Литература

1. Савельев И. В. Курс общей физики: Учебн. пособие для втузов: в 3 т. Т.1: 2.

2. Механика. Молекулярная физика. - 3-е изд., испр. - М.: Наука, 1986. – 432с.

3. Лабораторный практикум по физике: Учеб. пособие для студентов втузов/ Б. Ф. Алексеев, К. А. Барсуков, И. А. Войцеховская и др.; Под ред. К. А.                              Барсукова и Ю. И. Уханова. – М.: Высш. школа,1988. – 351 с.: ил.

    ISBN 5-06-001365-0

4. Майсова Н.Н. Практикум по курсу общей физики. – М.: Высшая школа, 1970

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ СИСТЕМЫ ТЕЛ

С ПОМОЩЬЮ МАЯТНИКА  ОБЕРБЕКА.

 Цель работы – определить момент инерции системы четырех одинаковых грузов массы  m  двумя способами: 1) экспериментально с помощью маятника Обербека, 2) теоретически, считая грузы материальными точками. Сравнить полученные результаты.

Приборы и принадлежности: маятник Обербека, секундомер, масштабная линейка, набор грузов, штангенциркуль.

Теоретическое введение

               Момент инерции – физическая величина, характеризующая инертность тела при вращательном движении.

                Моментом инерции материальной точки относительно оси вращения называется произведение массы этой точки на квадрат ее расстояния до оси (см. рис. 1)         

               Моментом инерции произвольного тела относительно оси называется сумма моментов инерции материальных точек  из которых состоит тело, относительно этой оси  (см. рис. 2) 

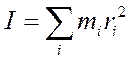
               Для однородных тел правильной геометрической формы можно заменить суммирование интегрированием.

,

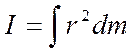где  dm = ρdV    (ρ – плотность вещества, dV– элемент объема)

          Таким образом получены формулы некоторых тел массой m относительно оси, проходящей через центр тяжести:

а) стержня длиной  относительно оси, перпендикулярной стержню

,

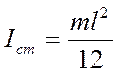б) обруча  (а также тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча и проходящей через его центр тяжести (совпадающей с осью цилиндра)

,

где  – радиус обруча (цилиндра)

в) диска (сплошного цилиндра) относительно оси, перпендикулярной плоскости диска и проходящей через его центр тяжести (совпадающей с осью цилиндра )

,

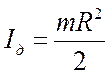где – радиус диска (цилиндра)

г) шара радиуса  R  относительно оси произвольного направления, проходящей через его центр тяжести

^.

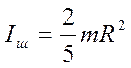 Момент инерции тела зависит: 1) от формы и размеров тела, 2) от массы и распределения масс, 3) от положения оси относительно тела.

               Теорема Штейнера о параллельных осях записывается как:

,

 где – момент инерции тела массой m относительно произвольной оси,  – момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно произвольной оси,  – расстояние между осями.

Описание установки

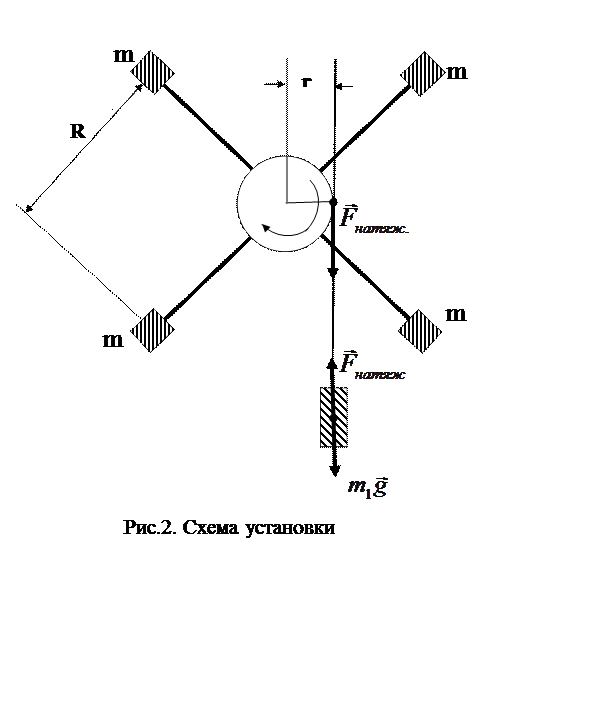
               Маятник Обербека представляет собой крестовину, состоящую из шкива и четырех равноплечих стержней, закрепленных на горизонтальной оси  (см. рис.2). На стержнях на равных расстояниях от оси вращения  насажены четыре одинаковых груза массы m каждый. При помощи груза m₁, прикрепленного к концу шнура, намотанного на один из шкивов, вся система может быть приведена во вращательное движение. Для отсчета высоты падения  h груза  m₁   имеется вертикальная шкала.

               Запишем второй закон Ньютона для падающего груза в векторной форме

                                          (1)

где  -  сила тяжести;      - сила натяжения шнура (см. рис. 1);

 - линейное ускорение, с которым падает груз m₁   вниз.

               Принимая направление движения груза за положительное, перепишем уравнение (I)  в скалярной форме

                                          (2)

откуда получим выражение для силы натяжения шнура

                                        (3)

               Линейное ускорение a находится из формулы пути равноускоренного движения без начальной скорости

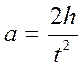                                                                 (4)

где h – высота падения груза m₁;      t – время падения.

               Сила натяжения нити F_нат вызывает ускоренное вращение крестовины. Основной закон вращательного движения крестовины с учетом сил трения запишется так :

M – M_тр = I× i    ,                                                          (5)