Методическое пособие для выполнения лабораторных работ по темам: Механика. Колебания и волны. Молекулярная физика, термодинамика, явления переноса, страница 3

На вертикальной оси ОО’ прибора укреплен блок Б₁ диаметром d, который при помощи намотанной на него нити и груза m можно привести во вращение. На этой же оси укреплена крестовина, состоящая из горизонтального стержня с массивными грузами  1 и 2 равной массы (m₁ = m₂). Крестовина и блок Б₁ вращаются как единое целое. Второй блок  Б_2, ось которого горизонтальна, служит для изменения направления нити. Установка снабжена тормозом Т и шкалой для измерения пути, пройденного грузом m. Вид сверху на блок Б₁ с намотанной на него нитью толщиной d показан на рис. 9.

Описание эксперимента (рис. 7)

При освобождении от тормоза груз m опускается равноускоренно из положения О в положение 1, проходя путь Н₁. Соответственно крестовина вращается равноускоренно. Это движение длится t₁ c. Затем груз m резко меняет направление скорости на противоположное и поднимается равнозамедленно из положения 1 в положение 2, пройдя путь Н₂ за время t₂ с. Соответственно крестовина вращается равнозамедленно, но в отличие от груза m не меняет направления своего движения. В положении О и 2 скорость груза  (а также и крестовины) равна 0. В положении 1 величина скорости груза не имеет определенного значения: при приближении к пункту 1 она больше, чем при удалении от него. Это является следствием частичной потери кинетической энергии. Экспериментальное определение Н₁, t₁ и Н₂, t₂ достаточно для независимых друг от друга расчетов  I, M и i, что позволяет проверить основной закон динамики для вращательного движения.

Расчет момента инерции крестовины.

                    Момент инерции крестовины относительно оси ОО’ не зависит от состояния ее движения и может быть рассчитан по формуле

I=I_гр+I_ст

где I_гр – момент инерции грузов m₁ и m₂, а I_ст – момент инерции стержня, на котором они закреплены. Поскольку m₁ = m₂, I_гр=2m₁R²,  где R – расстояние от оси ОО’ до центра груза, одинаковое для обоих грузов.

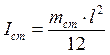, где  m_ст - масса стержня. Таким образом

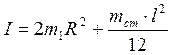                                                            (1)

Учет моментов сил, действующих на крестовину.

На каждом участке движения (ускоренном или замедленном) на крестовину действуют моменты двух сил: силы натяжения нити F_н и силы трения в опорных деталях конструкции. Обозначим эти моменты соответственно М и m. Для расчета М надо знать величину силы F_н и плечо h этой силы относительно оси вращения  ОО’. Силу F_н можно оценить, применив второй закон Ньютона к движению груза m.

В наших опытах ускорение грузa а<<g. Поэтому можно принять F_н=mg

Сложнее оценить плечо h.  Дело в том, что F_н не является сосредоточенной силой,  а распределена по поперечному сечению нити. Учитывая спиралевидный переплет волокон, из которых состоит нить, следует считать это распределение равномерным. Тогда распределенную силу F_н можно заменить сосредоточенной, действующей вдоль осевой линии нити (на рис.9 осевая линия обозначена пунктиром). Для сосредоточенной силы получим

h=0.5(d+d)

где     d - диаметр блока Б₁, а d – диаметр нити. Таким образом

M= F_н×0.5(d+d)=mg×0.5(d+d)= mgr                    (2)

Величина тормозящего момента m практически одинакова на всех участках движения. Это позволяет провести опыт так, чтобы исключить из рассмотрения момент m. Для участка ускоренного движения крестовины основной закон запишется в виде

I×i₁=M-m

Для участка замедленного движения будем иметь

I×i₂=M+m

где i₁ и i₂ -  угловые ускорения на первом и втором участке. Складывая два уравнения, получим  I(i₁+ i₂)=2M  или

M= I×i                                                 (3)

 где i=0.5(i₁+ i₂)

Уравнение (3) подлежит экспериментальной проверке.

Расчет угловых ускорений

Угловое ускорение i связано с ускорением a поступательного движения груза m. Поскольку v₀=v₂=0, то из формулы пути равнопеременного движения получим 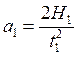 и 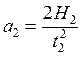 на участке ускоренного и замедленного движения  соответственно.

Все точки нити, расположенные в сечении xx’ (см. рис. 9), движущемся поступательно, имеют одинаковое ускорение, равное ускорению груза. Но точки нити, расположенные в сечении yy’, имеют разные тангенциальные ускорения, поскольку этот участок нити вращается вместе с блоком Б₁. Ускорение груза m совпадает с величиной тангенциального ускорения точки, лежащей на осевой линии нити (точка А на рис. 9). Радиус вращения точки А r_A=r=0.5(d+d).  Угловые ускорения i блока Б₁ и  i_A точки А одинаковы вследствие отсутствия проскальзывания нити. Пользуясь связью между угловым и тангенциальным ускорением точки А находим.

                             

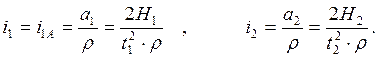
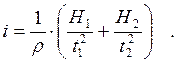                                                            (4)

Порядок выполнения работы.

1. Внимательно прочтите раздел «Описание эксперимента».

2. Измерьте расстояние Н₁ от нулевого деления шкалы до нижнего положения груза m при полностью раскрученной нити. Отсчет сделайте по верхнему краю груза m.

3. Установите грузы m₁ и  m₂ на одинаковом расстоянии R от оси вращения ОО’, указанном преподавателем.

4. Расположите верхний край груза m против деления ¢¢0¢¢ на шкале и зафиксируйте это положение тормозом. Установка готова к выполнению эксперимента.

5. Определите опытным путем отрезки времени t₁ и t₂. Для этого воспользуйтесь двумя секундомерами. Освободите тормоз и одновременно включите один из секундомеров. Когда груз опустится в крайнее нижнее положение, остановите работающий секундомер (отчет t₁)  и одновременно включите другой. Второй секундомер остановите, когда груз поднимется в положение 2, показанное на рис. 7 (отчет t₂) . Зафиксируйте груз в этом положении, включив тормоз. Сделайте отчет h по верхнему краю груза.

Если Вы работаете с одним секундомером, то отчеты  t₁ и t₂  придется делать при двух разных запусках  груза m.

6. Повторите указанные измерения 5 раз. Результаты занесите в табл. 1. Определите приближенные (средние) значения ,,  а также абсолютные погрешности Dt₁, Dt₂, Dh по методу Стьюдента. В эту же таблицу запишите измеренное в п. 2 значение Н₁ и выбранную величину R. Поскольку случайный разброс практически равен нулю,  , DH₁=1×10^{-2 м. ,} DR=5×10^{-3 м}

7. Запишите в таблицу 2 параметры экспериментальной установки, приближенные значения которые указаны на самом приборе.