Методическое пособие для выполнения лабораторных работ по темам: Механика. Колебания и волны. Молекулярная физика, термодинамика, явления переноса, страница 4

8. По формулам (1), (2) и (4) рассчитайте приближенные значения , , , подставив в них приближенные значения соответствующих величин, взятые из табл. 1 и 2. Определите приближенные значения произведения . Заполните табл. 3. Если , то формулу (3) можно считать подтвержденной.

9. Более строгим подтверждением формулы (3) является проверка доверительных интервалов величин М и  (J×i) на их перекрытие, наличие которого будет служить свидетельством справедливости проверяемого закона. Для этого надо рассчитать абсолютные погрешности DMи D(J×i) по формулам

,

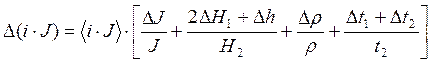
и записать доверительные интервалы в виде

 и  

Для наглядности эти интервалы рекомендуется изобразить на числовой оси.

Таблица 1.

Результаты измерений

№ п.п.	t1, c	t2, c	h, м	H1, м	R, м
1
2
3
4
5
D				1×10-2	5×10-3

  Таблица 2.

Параметры установки

	m1=m2,кг	l, м	mст, кг	m, кг	r, м
	431×10-3	510×10-3	111×10-3	152×10-3	10.4×10-3
D	1×10-3	5×10-3	1×10-3	1×10-3	0.1×10-3

Таблица 3.

Результаты вычислений

	H2, м	i, c-2	I, кг×м2	I×i	M, Н×м
D

Контрольные вопросы

1. Что называется угловой скоростью и угловым ускорением?  Их направление и единицы измерения.

2. Как в данной работе определялось угловое ускорение стержня с грузами? 

3. Что называется моментом инерции тела?  Единицы измерения момента инерции в системе СИ. От чего зависит величина момента инерции? 

4. Где должна проходить ось вращения, чтобы момент инерции тела был наименьшим?  Как рассчитать момент инерции тела относительно оси, не проходящей через его центр масс?  Как рассчитать момент инерции тела с грузами в данной работе? 

5. Что называется моментом силы относительно точки и относительно оси?  Единицы измерения момента силы.

6. В чем состоит основной закон динамики для вращательного движения?  Как этот закон проверялся в данной работе?

Литература

1. Савельев И. В. Курс физики. В 3 тт. СПб.: Издательство «Лань», 2008.

2. Детлаф А. А. , Яворский Б. М. Курс физики: Учебн. пособие для втузов. - М.: Высшая школа, 1989. - 607 с. - предм. указ.: с. 588-603.

3. Трофимова Т.И. Курс физики: учеб. пособие для вузов //Т.И. Трофимова. – 16-у изд., стер. – М.: Издательский цунтр «Академия», 2008. – 560с.

4. Биргер Б.Н. Приближения при вычислениях и измерениях. : Метод. указания к решению задач и выполнению лабораторных работ по физике - Иваново, ИХТИ, 1989 г. - 28с.

5. Бутман М.Ф., Кудин Л.С. Обработка и представление результатов измерений. Методические указания к лабораторному практикуму. - Иваново 2005. 36с.

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ

ФИЗИЧЕСКОГО МАЯТНИКА

          Цель работы: ознакомление с физическим маятником и определение его момента инерции относительно оси вращения. Изучение зависимости величины момента инерции маятника от пространственного распределения массы.

          Приборы и принадлежности: физический маятник с кронштейном для его подвеса, металлическая призма для определения положения центра тяжести маятника, секундомер.

Теоретическое введение.

Физическим маятником (рис.1) называется любое твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси (О), не проходящей через центр его тяжести (С). Точка подвеса маятника является центром вращения.

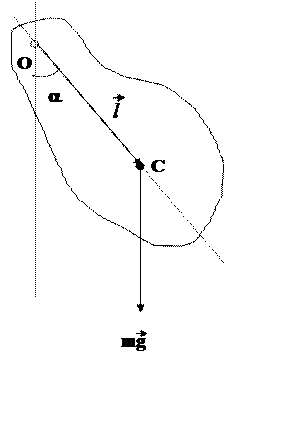Рис.1. Физический маятник

При отклонении маятника от положения равновесия на угол a возникает вращающий момент, созданный  силой тяжести:

,

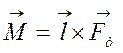
где l – расстояние между точкой подвеса и центром тяжести маятника (знак минус обусловлен тем, что момент силы М имеет такое направление, что стремится вернуть маятник к положению равновесия, т.е. уменьшить угол a).

Для малых углов отклонения , тогда

                                                                                                                 (1)

          С другой стороны момент возвращающей силы можно записать в виде:

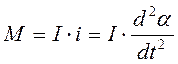                                                                                                          (2)

I – момент инерции маятника

i – угловое ускорение.

          Из (1) и (2) можно получить:

.

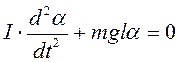
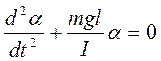Обозначая 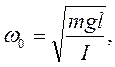                                                                                              (3)

получим 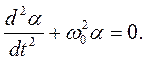                                                                              (4)

          Уравнение (4) – линейное дифференциальное уравнение 2-го порядка. Его решением является выражение .

          С учетом уравнения (3) период малых колебаний физического маятника можно записать как:

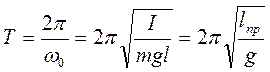,                                           (5)

где 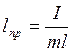  - приведенная длина физического маятника

          Из формулы (5) можно выразить момент инерции физического маятника относительно оси вращения

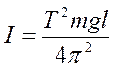                                                  (6)

          Находя путем измерений m, l и T, можно по формуле (6) вычислить момент инерции физического маятника относительно заданной оси вращения.

          В данной работе используется физический маятник (рис.2), представляющий собой стальной стержень, на котором закреплены две массивные стальные чечевицы (А₁ и А₂) и опорные призмы для подвеса (П₁ и П₂). Момент инерции такого маятника будет складываться из моментов инерции стержня, чечевиц и призм:

.

Момент инерции стержня можно рассчитать с помощью теоремы Штейнера:

,

где  I₀  - момент инерции стержня относительно оси, проходящей через центр тяжести.

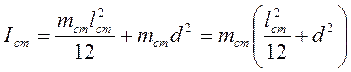                              (7)

          m_ст– масса стержня,