Коэффициент вязкости, в свою очередь, можно определить из закона Пуазейля, описывающего ламинарное течение вязкой среды в тонкой цилиндрической трубке.
Согласно закону Пуазейля объем газа/жидкости, протекающей через поперечное сечение трубки под действием перепада давления на концах трубки Dp, определяется выражением:
, (11)
где V – объем газа, r – радиус капилляра, l – длина капилляра, Dp – разность давлений на концах капилляра, t – время, в течение которого через капилляр протекает данный объем газа.
Из (3) получаем:
. (12)
Все величины, входящие уравнение (12) легко измеряются в опыте.
Средняя арифметическая скорость молекул газа <v> согласно молекулярно-кинетической теории определяется выражением:
, (13)
где R – универсальная газовая постоянная, Т – абсолютная
температура,
М – молярная масса.
Плотность газа r находится из уравнения Менделеева-Клапейрона:
, (14)
где P – давление газа.
После подстановки (12), (13) и (14) в (10) получаем:
. (15)
Разность давлений DP может быть рассчитана по формуле:
, (16)
где h1 и h2 – высоты уровней жидкости в сосуде А (рис. 4), g – ускорение свободного падения, rв – плотность воды.
Эффективный диаметр d молекулы находится из соотношения (3), в котором n – число молекул газа в единице объема при данных условиях. Для перехода к нормальным условиям (T0 = 273,15 K, P0 = 760 мм рт.ст. или 1,01325×105 Па) воспользуемся соотношением:
, (17)
Из (3) и (17) получаем выражение для эффективного диаметра молекулы газа:
. (18)
Описание установки
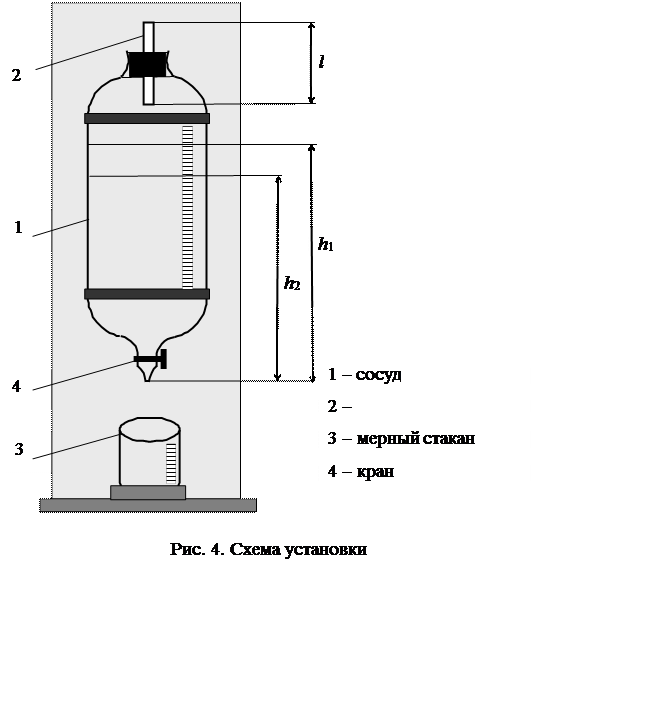
Для определения средней длины свободного пробега и эффективного диаметра молекул воздуха используется установка, состоящая из сосуда, заполненного водой (1), капилляра (2) и мерного стакана (3) (рис. 1). Если открыть кран, то вода будет выливаться из сосуда, одновременно через капилляр в сосуд будет засасываться воздух. Таким образом, капилляр является той трубкой, в которой устанавливается ламинарное течение воздуха в результате того, что разные концы трубки находятся под разным давлением (верхний конец – под атмосферным давлением, нижний – меньше атмосферного). Сосуд снабжен шкалой, с помощью которой можно определить высоту столба вытекшей воды. Под сосудом устанавливается мерный стакан для определения объема вытекшей воды, равного объему воздуха, поступившего в сосуд.
Порядок выполнения работы
1. Поставить под сосуд химический стакан, открыть кран, прикрыв пальцем капилляр. Дождавшись, когда вода перестанет вытекать из сосуда, заменить химический стакан мерным стаканом.
2. Отметить по шкале начальную высоту уровня воды h1 в сосуде, отпустить палец, освободив капилляр, и одновременно включить секундомер.
3. Через время t = 30 – 120 секунд (выбирается в зависимости от емкости сосуда и параметров капилляра) закрыть кран (4) и одновременно остановить секундомер.
4. Записать время истечения жидкости t, конечную высоту уровня воды h2 в сосуде и объем вытекшей воды V.
5. Все измеренные величины занести в таблицу экспериментальных данных.
6. Повторить опыт пять раз.
7. Измерить и записать температуру в комнате и атмосферное давление.
8. Вычислить DP по формуле (16).
9. Найти для каждого опыта среднюю длину свободного пробега и эффективный диаметр молекул воздуха по формулам (15) и (18).
10. Вычислить средние значения длины свободного пробега <l> и эффективного диаметра d молекул воздуха и рассчитать случайные погрешности Dl и Dd. Вычисленные величины занести в таблицу экспериментальных данных.
11. Записать окончательный результат в виде:
l = <l> ± Dl (м).
d = <d> ± Dd (м).
12. Сравнить полученные значения величин l и d с литературными данными и сделать выводы по работе.
Таблица
Результаты измерений и вычислений
|
№ п/п |
t (c) |
V (м3) |
h1 (м) |
h2 (м) |
Тк (К) |
Р (Па) |
DР (Па) |
l (м) |
d (м) |
|
1 |
|||||||||
|
2 |
|||||||||
|
3 |
|||||||||
|
4 |
|||||||||
|
5 |
|||||||||
|
Среднее значение |
|||||||||
|
Случайная погрешность |
|||||||||
Примечание: R = 8,314 Дж/моль×К;
Мвозд = 28,96×10–3 кг/моль;
n0 = 2,69×1025 м–3;
1 мм рт. ст. = 133,3 Па.
Радиус r и длина l капилляра указаны на установке.
Контрольные вопросы
1. Что такое средняя длина свободного пробега молекулы?
2. От каких факторов зависит средняя длина свободного пробега молекулы?
3. На чем основано определение средней дины свободного пробега в данной работе?
4. Каков физический смысл эффективного диаметра молекул?
5. Явления переноса: теплопроводность, диффузия, вязкость. В чем суть явлений?
6. Какова связь между коэффициентами теплопроводности, диффузии и вязкости.
7. Какое явление описывает закон Пуазейля?
Литература:
Савельев И.В. Курс общей физики. Учеб. Пособие. В 3-х т. Т.1. Механика. Молекулярная физика. – 3-е изд., испр. – М.: Наука. Гл. ред. физ. мат. лит. 1986. 432 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.