Методическое пособие для выполнения лабораторных работ по темам: Механика. Колебания и волны. Молекулярная физика, термодинамика, явления переноса, страница 10

Контрольные вопросы и задания

1.  Какие колебания называются гармоническими? Под действием какой силы они происходят? Запишите второй закон Ньютона для гармонических колебаний.

2.  Запишите уравнение смещения от времени для гармонического колебания. Перечислите величины, характеризующие гармоническое колебание. Изобразите график гармонического колебания.

3.   Какие колебания называются затухающими? Запишите второй закон Ньютона для затухающих колебаний.

4.  Запишите уравнение смещения от времени для затухающего колебания. Перечислите величины, характеризующие затухающее колебание. Изобразите график затухающего колебания.

5.  Дайте определение логарифмического декремента колебаний. Каков его физический смысл? Как он определяется в данной работе, от чего зависит?

Литература

1. Савельев И. В. Курс общей физики: Учебн. пособие для втузов: в 3 т. Т.1: Механика. Молекулярная физика. - 3-е изд., испр. - М.: Наука, 1986. – 432с.

2. Детлаф А. А. , Яворский Б. М. Курс физики: Учебн. пособие для втузов. - М.: Высшая школа, 1989. - 607 с. - предм. указ.: с. 588-603.

3. Майсова Н.Н. Практикум по курсу общей физики. – М.: Высшая школа, 1970

4. Лабораторный практикум по физике: Учеб. пособие для студентов втузов./ Ахматов А.С., Андреевский В.М., Кулаков А.И. и др.; Под редакцией А.С. Ахматова. – М.: Высшая школа. 1980. – 360 с.

ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКА В ВОЗДУХЕ
МЕТОДОМ СТОЯЧИХ ВОЛН

Цель работы: определение длины стоячей волны и скорости звука в воздухе.

Приборы и принадлежности: резонатор с телефоном и микрофоном, звуковой генератор, осциллограф, отсчетная линейка.

Теоретическое введение

          Звук представляет собой упругие волны, распространяющиеся в газах, жидкостях и твердых телах и воспринимаемые ухом человека и животных. Человеческое ухо способно воспринимать звук с частотами от 16 Гц до 20 кГц. Звук с частотами ниже 16 Гц называется инфразвуком, а выше 20 кГц – ультразвуком. Наука о звуке называется акустикой.

          Если в упругую среду поместить источник колебаний, то соприкасающиеся с ним частицы будут выведены из положения равновесия и придут в колебательное движение. Колебания этих частиц передаются силами упругости соседним частицам среды, а от них – к другим, более удаленным от источника колебаний. Через некоторое время колебательный процесс охватит всю среду. Распространение колебаний в упругой среде называется волной или волновым процессом.

          Различают продольные волны (частицы колеблются вдоль направления распространения волны) и поперечные волны (частицы колеблются перпендикулярно этому направлению). Продольные волны представляют собой чередующиеся сгущения и разрежения. Такие волны распространяются в средах, в которых возникают силы упругости при деформациях сжатия и растяжения, но не обладающих напряжением сдвига (т.е. в твердых телах, жидкостях и газах). Примером продольных волн являются звуковые волны. Поперечные волны распространяются в средах, в которых возникают упругие силы при деформации сдвига (т.е. в твердых телах или в некоторых особых случаях, например, волны на границе раздела жидкость-газ). Скорость распространения продольных и поперечных волн зависит от упругих свойств среды. Так, при 20 ºС скорость звука в воздухе равна 343 м/c, в воде – 1480 м/c, в стали – около 6000 м/c.

Скорость звука в газах теоретически можно рассчитать по формуле:

,                                                          (1)

где g – показатель адиабаты (отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме), R – молярная газовая постоянная, Т – термодинамическая температура, М – молярная масса газа. Таким образом, скорость звука в газах оказывается такого же порядка, что и средняя скорость теплового движения молекул.

Уравнение бегущей волны, распространяющейся вдоль координаты x, имеет вид:

x = Acos(wt – kx),                                                   (2)

где x – смещение частиц среды от положения равновесия; А – амплитуда волны; w – циклическая частота колебаний; t – время; k – волновое число, 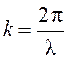 (l – длина волны).

          Стоячей волной называется особое колебательное состояние среды, возникающее при наложении двух встречных бегущих волн (например, прямой и отраженной) одинаковой амплитуды и частоты. Стоячая волна – это частный случай интерференции волн.

          Рассмотрим сложение двух встречных волн с одинаковой амплитудой и частотой. Прямая волна описывается уравнением

x₁ = Acos(wt – kx),                                                           (3)

в уравнении отраженной волны координата x меняет знак на противоположный:

x₂ = Acos(wt + kx).                                                           (4)

Сложим уравнения (3) и (4):

x = x₁ + x₂ = Acos(wt – kx) + Acos(wt + kx)

и, воспользовавшись формулой для суммы косинусов двух углов, получим уравнение стоячей волны:

x = 2Acosxcoswt.                                              (5)

Выражение, стоящее перед coswt, представляет собой амплитуду стоячей волны:

А_{ст. в.} = | 2Acosx |.                                              (6)

Амплитуда колебаний частиц среды в стоячей волне зависит от координаты частиц x и, следовательно, меняется от точки к точке. Амплитуда стоячей волны максимальна (такие геометрические места называются пучностями) при условии

cosx = ± 1,

т.е.

x = ± pn,                                                           (7)

откуда координаты пучностей

x_пучн = ± .                                               (8)

Амплитуда стоячей волны принимает нулевые значения (такие точки называются узлами) при условии

                   cosx = 0,

т.е.

x = ± (2n + 1),                                    (9)

откуда координаты узлов

x_узл= ± 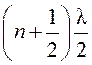.                                        (10)

          В формулах (7) – (10) n = 0, 1, 2, 3 … . Расстояние между соседними узлами или соседними пучностями равно l/2, а соседние узлы и пучности сдвинуты на l/4. Точки, находящиеся в узлах, не совершают колебаний.