Методическое пособие для выполнения лабораторных работ по темам: Механика. Колебания и волны. Молекулярная физика, термодинамика, явления переноса, страница 14

4. Методические указания к выполнению лабораторных работ по разделу “Механика“.-   Иваново, ИХТИ, 1989 г. (под редакцией Биргера Б.Н.). 

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ

Цель работы – в работе требуется определить коэффициент вязкости глицерина по методу Стокса.

Приборы и принадлежности: труба с глицерином, масштабная линейка, шарики, микрометр и секундомер.

Теоретическое введение.

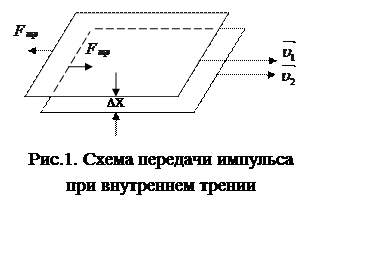          Если привести один слой жидкости в упорядоченное движение со скоростью u₁, то он увлечет за собой прилегающий слой со скоростью u₂, последующий со скоростью u₃ и т.д. При этом скорость упорядоченного движения убывает в перпендикулярном направлении к движению слоев жидкости, т.е. u₁>u₂>u₃… . Выделим два слоя жидкости на расстоянии Dx друг от друга, движущихся со скоростями и  (см. рис.1).

Вследствие передачи импульса при переходе молекул из слоя в слой возникает сила внутреннего трения.

Сила внутреннего трения пропорциональна площади соприкосновения взаимодействующих слоев жидкости и градиенту скорости

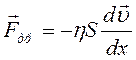,                                                       (1)

где - коэффициент динамической вязкости жидкости (или просто вязкость); S - площадь слоя;  - градиент скорости.

Коэффициентом динамической вязкости называется величина, численно равная силе внутреннего трения, с которой один слой увлекает или тормозит другой слой жидкости при условии, что площадь соприкосновения слоев  и градиент скорости .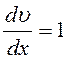

В системе СИ за единицу динамической вязкости принимают 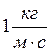  - вязкость такой среды, в которой один слой увлекает или тормозит другой с силой в , если площадь соприкосновения слоев  и градиент скорости .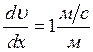

Коэффициентом кинематической вязкости  называется отношение коэффициента динамической вязкости к плотности жидкости

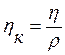.                                                         (2)

          Коэффициент вязкости существенно зависит от температуры. Для жидкости с повышением температуры он резко уменьшается.

Определение коэффициента динамической вязкости методом Стокса

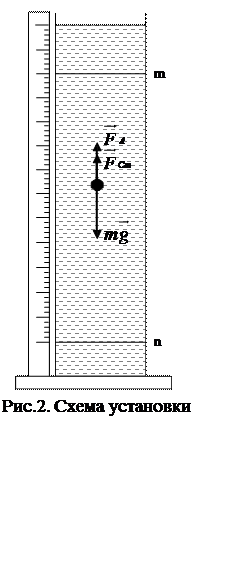
          Рассмотрим свободное падение тела внутри покоящейся жидкости. Пусть в сосуде с жидкостью вертикально падает небольшой шарик радиуса  с малой скоростью  (см. рис. 2). В этом случае между тонким слоем жидкости, обволакивающим шарик, и окружающей средой возникает сила внутреннего трения. Последняя направлена против движения и, согласно закону Стокса, равна

,                           (3)

где  - коэффициент вязкости жидкости.

          Кроме указанной силы , на шарик действуют две силы – сила тяжести (вертикально вниз) и сила Архимеда  (вертикально вверх).

          В первый момент падения шарик движется равноускоренно, так как сила тяжести больше суммы сил, действующих вертикально вверх. При дальнейшем падении скорость шарика увеличивается, возрастает и сила внутреннего трения (см. формулу 3). Когда скорость шарика будет иметь такое значение, при котором все три силы ,  и   уравновешиваются (сумма сил равна нулю), тогда шарик согласно первому закону Ньютона, будет падать равномерно с постоянной скоростью .

          Для этого случая имеем

.                                              (4)

          Обозначим через  плотность шарика, а через  - плотность жидкости. Если силу тяжести выразить через плотность, то получим

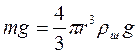.                                             (5)

Соответственно сила Архимеда

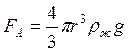.                                               (6)

          Подставляя значения сил (3), (5) и (6) в (4) и выражая , найдем

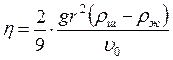.                                                 (7)

          По формуле (7) можно вычислить коэффициент вязкости жидкости, если измерить на опыте скорость равномерного движения шарика в жидкости. Для этой цели необходимо измерить время t прохождения шариком расстояния l между метками m и n (см. рис.2). Скорость равномерного движения будет , и расчетная формула примет вид

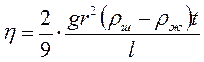.                                  (8)

Порядок выполнения работы

1.  При помощи микрометра измерить пять-шесть раз диаметр шарика, вычислить из полученных данных среднее значение и занести в таблицу радиус шарика. Аналогично найти радиусы еще четырех шариков.

2.  Выбрать расстояние между метками m и n

3.  По секундомеру отметить время движения каждого шарика от верхней до нижней метки.

4.  По формуле (8) рассчитать коэффициент вязкости глицерина для каждого опыта, результаты занести в таблицу.

5.  Вычислить приближенное значение коэффициента вязкости h, абсолютную и относительную погрешности.

6.  Окончательный результат записать в виде

.

Таблица

Результаты измерений и вычислений

№ п/п	Радиус шарика r, м	Время падения шарика t, с	Расстояние между метками l, м	Коэффициент вязкости h,
1 2 3 4 5
Приближенное значение
Абсолютная погрешность

Контрольные вопросы

1.  Что называется коэффициентом вязкости? Единицы измерения вязкости.

2.  От каких факторов зависит коэффициент вязкости жидкости?

3.  Сущность метода Стокса для определения коэффициента вязкости жидкости с выводом расчетной формулы.

4.  Обосновать изменение скорости движения шарика с увеличением его диаметра?

Литература

1. Детлаф А. А. , Яворский Б. М. Курс физики: Учебн. пособие для втузов. - М.: Высшая школа, 1989. - 607 с. - предм. указ.: с. 588-603.

2. Лабораторный практикум по физике: Учеб. пособие для студентов втузов/ Б. Ф. Алексеев, К. А. Барсуков, И. А. Войцеховская и др.; Под ред. К. А.                              Барсукова и Ю. И. Уханова. – М.: Высш. школа,1988. – 351 с.: ил.

    ISBN 5-06-001365-0

3. Трофимова Т.И.  Курс физики. - М.: Высшая школа , 1990г.

ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА И ЭФФЕКТИВНОГО ДИАМЕТРА МОЛЕКУЛ ВОЗДУХА

Цель работы: определить среднюю длину свободного пробега и эффективный диаметр молекул воздуха по коэффициенту внутреннего трения.