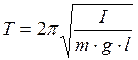Методическое пособие для выполнения лабораторных работ по темам: Механика. Колебания и волны. Молекулярная физика, термодинамика, явления переноса, страница 6

                                              (2),

где I– момент инерции маятника относительно горизонтальной оси, проходящей через точку подвеса; m– масса маятника; l– расстояние между точкой подвеса и центром масс маятника.

Сопоставление формул (1) и (2) показывает, что математический маятник с длиной

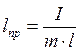                                                       (3)

будет иметь такой же период колебаний, как и данный физический маятник. Величину (3) называют приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Этот период задается формулой:      

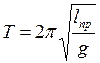                                                    (4).

Точка О' на прямой, соединяющей точку подвеса О с центром масс C, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (рис. 1). Приведенная длина всегда больше l, поэтому точка подвеса и центр качания лежат по разные стороны от центра масс.

Можно показать, что при подвешивании маятника в центре качания О' приведенная длина маятника, а значит и его период колебаний, будут теми же, что и вначале (когда маятник был подвешен в точке О). Следовательно, точка подвеса О и центр качания О' обладают свойством взаимозаместимости: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.

На этом свойстве основано определение ускорения свободного падения с помощью так называемого оборотного маятника. Оборотным называют такой физический маятник, у которого имеются две параллельные друг другу, закрепленные вблизи его концов опорные призмы, за которые маятник можно поочередно подвешивать. Закрепленные на маятнике тяжелые грузы можно перемещать вдоль маятника. Перемещением грузов можно добиться того, чтобы при подвешивании маятника за любую из опорных призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно приведенной длине физического маятника l_пр. Измерив период колебаний маятника и зная l_пр , можно по формуле (4) найти ускорение

свободного падения g.

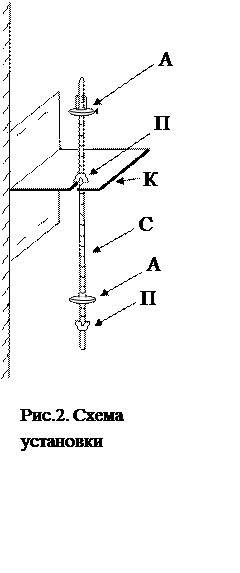
Описание установки

Используемый в данной работе оборотный маятник изображен на рисунке 2. Маятник представляет собой стальной стержень С, снабженный двумя неподвижными опорными призмами П₁ и П₂. На стержне закреплены две массивные стальные чечевицы A₁ и A₂. Чечевицу A₂  можно перемещать вдоль стержня и закреплять в различных положениях, определяемых расстоянием b от конца стержня. Маятник подвешивают на кронштейне К поочередно за каждую из призм П₁ и П₂. Перемещением чечевицы A₂ добиваются того, чтобы при подвешивании на призмах П₁ и П₂ период колебаний маятника был одинаков. Тогда расстояние между опорными ребрами призм будет равно приведенной длине l_пр.

Порядок выполнения работы

1.  Закрепите чечевицу А₂ на некотором расстоянии b от конца стержня.

2. Установите маятник на опорной призме П₁. Приведите маятник в колебательное движение, отклонив его на небольшой угол (не более 10°) от вертикальной оси. Найдите период колебаний 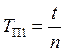, трижды определив время t, за которое маятник совершает n колебаний (рекомендуем взять n  = 10), и вычислив среднее арифметическое t_ср. Результаты измерений и вычислений занесите в таблицу 1.

3. Установите маятник на опорной призме П₂ и проведите измерения периода колебаний 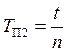  так же,  как описано в пункте 2.

Опыты (1-3) рекомендуем провести при пяти–шести (k = 5¸6) положениях чечевицы А₂, например, соответствующих расстояниям b₁ = 2, b₂ = 6, b₃ = 10, b₄ = 14, b₅ = 18 см.

4. Постройте графики Т_П1 = f₁(b) и Т_П2 = f₂(b) зависимостей периода колебаний маятника от положения чечевицы А₂, откладывая по оси абсцисс расстояние b, а по оси ординат периоды колебаний Т_П1 и Т_П2, измеренные при различных значениях b при двух положениях маятника (с опорой на призму П₁ и на призму П₂). Координата b_x точки пересечения кривых Т_П1 = f₁(b) и Т_П2 = f₂(b) определяет такое положение чечевицы А₂, при котором периоды Т_П1 и Т_П2 одинаковы: Т_П1 = Т_П2 = Т.

5. Уточните значение периода колебаний маятника Т при найденном положении b_x чечевицы А₂. Для этого закрепите чечевицу А₂ в положении b_x и, подвесив маятник сначала на призме П₁, а потом на призме П₂, по три раза измерьте соответствующие времена t₁ и t₂, за которые маятник совершает n колебаний (во всех опытах возьмите одно и то же значение n = 10). Вследствие погрешности определения расстояния b_x величины Т_П1 и Т_П2, а следовательно и величины t₁ и t₂, могут отличаться друг от друга. Необходимое для вычисления периода колебаний 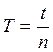 наиболее вероятное значение t времени n колебаний, а также абсолютную погрешность Δt величины t найдите методом Стьюдента, используя шесть измеренных значений t (трех величин t₁ и трех величин t₂). Результаты измерений и расчетов занесите в таблицу 2.

6. Определите приведенную длину маятника l_пр, измерив расстояние между ребрами опорных призм (при измерении можно использовать нанесенные на стержень маятника сантиметровые метки).

7. Вычислите g по формуле:   .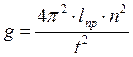

8. Вычислите относительную погрешность определения величины g по формуле:

,

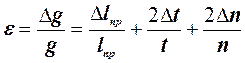при этом погрешность Δn определения числа колебаний можно принять равной нулю.

9. Найдите абсолютную погрешность:

Δg = ε·g .

10. Запишите окончательный результат:

g = (g ± Δg);  ε  = . . .    .

Сравните этот результат с величиной ускорения свободного падения, приводимой в справочниках по физике: g = 9.80665 м/с².

Таблица 1

Измерения периода колебаний оборотного маятника при опоре на призму П₁ и на призму П₂ при различных положениях b чечевицы А₂

b, см	№	Призма П1			Призма П2
		t, с	tср, с	T, с	t, с	tср, с	T, с
b1	1 2 3
b2	1 2 3
·       ·       ·
bk	1 2 3