где М – момент силы натяжения; Mтр - момент сил трения; I - момент инерции крестовины; i - угловое ускорение, с которым вращается крестовина. Величина момента сил трения Mтр по сравнению с величиной вращающего момента М невелика, и, следовательно, ею можно пренебречь.
Из уравнения ( 5 ) с учетом сделанного замечания получаем окончательную формулу для расчета момента инерции крестовины
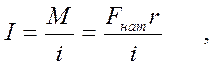 (6)
(6)
где r - радиус шкива. Угловое ускорение i определяется по формуле
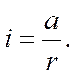 (7)
(7)
Подставляя (3) и (7) в (6), получаем окончательную формулу для расчета момента инерции крестовины
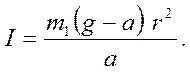 (8)
(8)
Порядок выполнения работы.
Часть I.
Экспериментальное определение момента инерции системы 4х грузов.
1. Снять со стержней грузы m .
2. Намотать в один слой шнур на шкив, установив груз m1 на заранее выбранной высоте h. Отпустив крестовину, замерить время падения tо груза с помощью секундомера. Опыт повторить пять раз (при одной и той же высоте падения h ).
3. Закрепить на концах стержней грузы m.
4. Выполнить операции, указанные в пункте 2, измеряя секундомером время падения t. Опыт повторить пять раз.
5. С помощью штангенциркуля измерить диаметр шкива d в пяти разных положениях.
6. Результаты измерений занести в таблицу. Найти приближенные значения и по методу Стьюдента оценить абсолютные погрешности измерения величин tо, t и d.
7. По формуле (4) рассчитать величину линейного ускорения a, с которым падает груз m1 для случаев:
а) крестовина без грузов (aо),
б) крестовина с грузами (а).
8. По формуле (8) вычислить момент инерции крестовины без грузов (Io) и с грузами (I), используя приближенные значения m1, R, g и полученные значения а и ао.
9. Вычислить погрешности измерений по формулам:
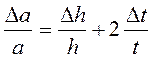 (9)
(9)
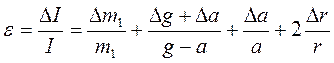 (10)
(10)
Таблица 1
Результаты измерений и вычислений
|
№ п/п |
to, c |
t, c |
d, м |
h, м |
m = (0,144+0,005) кг m1 = (0,175+ 0,005) кг R = (0,220 + 0,003) м |
|
1 2 3 4 5 |
|||||
|
Приближен. значения |
|||||
|
Абсолютная погрешность |
Часть II.
1. Теоретически найти момент инерции системы 4х грузов массы m, находящихся на расстоянии R от оси вращения (считая грузы материальными точками)
![]() (11)
(11)
2. Сравнить результаты эксперимента и расчетов. Вычисть относительную погрешность
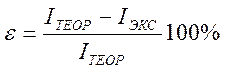 (12)
(12)
и сделать вывод о том, как велико расхождение полученных результатов.
Контрольные вопросы.
1. Что называется моментом инерции материальной точки и произвольного тела?
2. От чего зависит момент инерции тела относительно оси вращения?
3. Приведите примеры формул момента инерции тел. Как они получены?
4. Теорема Штейнера о параллельных осях и ее практическое использование.
5. Вывод формулы для расчета момента инерции крестовины с грузами и без грузов.
1. Савельев И. В. Курс общей физики: Учебн. пособие для втузов: в 3 т. Т.1: Механика. Молекулярная физика. - 3-е изд., испр. - М.: Наука, 1986. – 432с.
2. Детлаф А. А. , Яворский Б. М. Курс физики: Учебн. пособие для втузов. - М.: Высшая школа, 1989. - 607 с. - предм. указ.: с. 588-603.
3. Зисман Г. А., Тодес О. М.. Курс общей физики для втузов: в 3 т. Т. 1: Механика, молекулярная физика, колебания и волны - 4-е изд., стереотип. - М.: Наука, 1974. - 340 с.
4. Методические указания к выполнению лабораторных работ по разделу “Механика“.- Иваново, ИХТИ, 1989 г. (под редакцией Биргера Б.Н.).
Часть II. Колебания и волны
ОПРЕДЕЛЕНИЕ ЛОГАРИФМИЧЕСКОГО ДЕКРЕМЕНТА
КОЛЕБАНИЙ МАЯТНИКА
Цель работы: определить логарифмический декремент колебаний маятника при наличии разных сил сопротивления и построить графики изменения амплитуды колебаний со временем.
Приборы и принадлежности: маятник, кювета со шкалой, приспособление для пуска маятника, секундомер, емкость с водой.
Колебаниями называются движения или процессы, повторяющиеся во времени. Простейшим видом колебательного движения является гармоническое колебание. Оно возникает в том случае, когда на тело, выведенное из положения равновесия, действует сила F, направленная к положению равновесия и пропорциональная смещению:
F = –kx, (1)
где х – смещение тела от положения равновесия, k – коэффициент пропорциональности, который зависит от упругих свойств системы и называется коэффициентом квазиупругой силы. Знак минус показывает, что сила направлена противоположно смещению.
Второй закон Ньютона для материальной точки, совершающей гармоническое колебание, представляет собой дифференциальное уравнение второго порядка
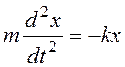 , (2)
, (2)
где m – масса материальной точки.
Решением уравнения (2) является выражение
x = Acos(wt + a), (3)
где A – амплитуда колебаний, w – циклическая частота, a – начальная фаза колебаний. Аргумент периодической функции
j = wt + a (4)
называется фазой колебаний. При t = 0 фаза j = a. Начало отсчета можно выбрать так, чтобы a = 0, тогда
x = Acoswt. (5)
График зависимости смещения х от времени t представляет собой график гармонического колебания (рис. 1).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.