lст – длина стержня,
d – расстояние от центра тяжести стержня до точки подвеса.
Моменты инерции чечевиц и призм можно приближенно рассчитать как для точечных масс. Тогда момент инерции маятника запишется в виде:
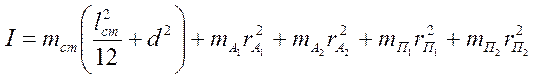, (8)
где 
- массы чечевиц А1 и А2,
- расстояния от оси вращения (точки
подвеса) до чечевиц А1 и А2 соответственно,
- массы призм П1 и П1,
- расстояния от оси вращения до призм
П1 и П2 соответственно.
Т.к.
по условиям выполнения работы перемещается лишь одна чечевица А1, то
изменяться будет лишь момент инерции 
и
(9)
Описание установки.
Применяемый в данной работе физический маятник (рис.2) представляет собой стальной стержень (С), на котором закреплены две массивные стальные чечевицы (А1 и А2) и опорные призмы для подвеса (П1 и П2). Маятник подвешивается на кронштейне.
Посредством перемещения одной из чечевиц можно изменить момент инерции маятника относительно точки подвеса (оси вращения).
Центр тяжести маятника определяется балансированием маятника на горизонтальном ребре специальной призмы (рис.3). На стержне маятника через 10 мм нанесены кольцевые нарезки, служащие для точного определения расстояния от центра тяжести до оси вращения без помощи линейки. Небольшим смещением чечевицы А1 вдоль стержня можно добиться, чтобы расстояние l от точки подвеса до центра тяжести равнялось целому числу сантиметров, отсчитываемому по шкале на стержне.
Порядок выполнения работы.
1. Определить положение центра тяжести маятника.
а) Снять маятник с кронштейна и установить его в горизонтальном положении на специальной призме П3 (рис.3) так, чтобы он находился в равновесии. Точное положение равновесия достигается небольшим передвижением чечевицы А1.
 |
Рис.3. Уравновешивание маятника
б) По шкале на маятнике измерить l - расстояние от точки подвеса (ребро призмы П1) до центра тяжести маятника (верхнее ребро призмы П3).
в) По шкале маятника измерить расстояние 
- от точки подвеса (ребро призмы П1) до верхней
чечевицы А1.
2. Определить период колебаний физического маятника.
а) Установить маятник призмой П1 на кронштейн (рис.2)
б) Определить время полных 50 - 100 колебаний маятника. Записать время t и число n колебаний маятника.
в) Определить период колебаний физического маятника по формуле:
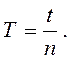(10)
3. Снять маятник с кронштейна. Передвинуть чечевицу А1 на несколько сантиметров в новое положение и повторить опыт. Измерения должны быть выполнены не менее, чем для трех различных положений чечевицы А1 относительно точки подвеса.
4. По формуле (6) вычислить момент инерции физического маятника Iоп.
5. Вычислить относительную погрешность момента инерции для одного из рассмотренных случаев по формуле:
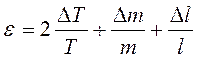. (11)
Величины DT и Dl определяются по классу точности приборов.
6. Найти абсолютную погрешность 
для
каждого случая, принимая относительную погрешность одинаковой для всех
случаев.
Записать в таблицу окончательный результат в виде
7. По формуле (8) вычислить момент инерции маятника Iтеор для каждого случая.
8. Сравнить полученные результаты Iоп и Iтеор, вычислив отношение:
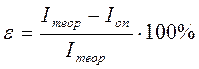(12)
Сделать вывод о том, насколько велико расхождение полученных значений и каковы причины расхождений.
Таблица
Результаты измерений и вычислений
|
№ п/п |
l, м |
t, с |
n |
T, c |
м |
|
Iтеор, кг м2 |
|
|
1 2 3 |
Контрольные вопросы.
1. Что такое физический маятник?
2. Что называется приведенной длиной физического маятника?
3. Какое колебание называется гармоническим?
4. Что такое период колебаний?
5. Выведите формулу для вычисления периода колебаний физического маятника.
6. Что такое момент инерции? В чем заключается аддитивность момента инерции?
7. Как рассчитать момент инерции тела относительно оси, не проходящей через центр его тяжести?
8. Получите формулу для вычисления момента инерции физического маятника.
Литература
1. Савельев И. В. Курс общей физики: Учебн. пособие для втузов: в 3 т. Т.1: Механика. Молекулярная физика. - 3-е изд., испр. - М.: Наука, 1986. – 432с.
2. Детлаф А. А. , Яворский Б. М. Курс физики: Учебн. пособие для втузов. - М.: Высшая школа, 1989. - 607 с. - предм. указ.: с. 588-603.
3. Лабораторный практикум по физике: Учеб. пособие для студентов втузов/ Б. Ф. Алексеев, К. А. Барсуков, И. А. Войцеховская и др.; Под ред. К. А. Барсукова и Ю. И. Уханова. – М.: Высш. школа,1988. – 351 с.: ил.
ISBN 5-06-001365-0
4.Майсова Н.Н. Практикум по курсу общей физики. – М.: Высшая школа, 1970
Определение ускорения свободного падения
с помощью оборотного маятника
Цель работы: познакомиться с оборотным маятником и определить с его помощью ускорение свободного падения.
Приборы и принадлежности: оборотный маятник, секундомер.
Маятником называют твердое тело, способное под действием силы тяжести совершать колебания вокруг неподвижной точки или оси. Принято различать математический и физический маятники.
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена материальная точка (тело, размерами которого можно пренебречь). Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити. Период колебаний математического маятника равен:
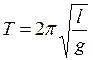(1),
где l– длина маятника, g– ускорение свободного падения.
Физическим маятником называется твердое тело, укрепленное на неподвижной горизонтальной оси, не проходящей через его центр масс. Под действием силы тяжести физический маятник способен совершать колебания относительно этой оси. При малых колебаниях период колебаний физического маятника определяется формулой:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
