Кинематика, динамика и конструирование привода поршневого компрессора, страница 9

При построении планов скоростей и в дальнейшем, планов ускорений на практике часто применяют теорему подобия: «отрезки и фигуры, образованные точками на плане положений механизма подобны (пропорциональны) и сходственно распложены  по отношению к отрезкам и фигурам ни планах скоростей и ускорений; причем полученные фигуры на планах скоростей и ускорений относительно одноименных фигур на планах положений повернуты на 90 º». План скоростей удобно строить в масштабе кривошипа, или в масштабе кратном масштабу кривошипа. Масштабный коэффициент μ_υ равен отношению действительной скорости.

Для построения плана скоростей выбирается масштабный коэффициент равный отношению действительной величины скорости к длине отрезка на чертеже.

μ_υ=μ_l·ω₁                                                                                                    (4)

Векторы на плане скоростей обозначают строчными латинскими буквами α,b,c,d,e…

Для построения планов скоростей данного механизма поршневого компрессора будем использовать масштаб двух кривошипов, т.е. μ_υ=(μ_l/2)·ω_1..  Угловую скорость ω₁ определим по формуле:

ω₁=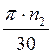                                                                                                        (5)

ω₁=(3,14·51)/30=5,338(1/с);

μ_υ=(0,004/2) ·5,338=0,0107(м/с·мм)

Обозначим на чертеже полюс р.

Составляем векторные уравнения:

υ_А=0,                                                                                                            (6)

так как эта точка принадлежит стойке, поэтому она совпадет с полюсом р.

υ_в= υ_А+υ_В/А                                                                                                     (7)

Откладываем от точки А(р) отрезок аb=2АВ перпендикулярно звену АВ с плана положений по направлению угловой скорости первого звена.

υ_С= υ_В+υ_С/В                                                                                                    (8)

υ_С= υ_С0+υ_{С/ С0}                                                                                                (9)

υ_С0 =0,                                                                                                          (10)

поэтому точка С₀ совпадет с полюсом р.

Точку с находим на пересечении перпендикуляра к ВС с плана положений через точку b на плане скоростей и горизонтали х – х.

Точку d на плане скоростей можно найти по теореме подобия:

=

bd=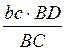                                                                                                    (11)

υ_Е= υ_D+υ_E/D                                                                                                  (12)

υ_E= υ_E0+υ_E/E0                                                                                                (13)

υ_E0=0,                                                                                                           (14)

поэтому точка Е₀ попадет в р.

Точку Е находим как точку пересечения перпендикуляра к DЕ с планов положений через d на плане скоростей и горизонтали  х – х.

На рисунке 6 показан план скоростей для 2 положения.

b

                                            d

                         c                                                      p,a

Рисунок 6 - Пример планов скоростей

Соединив одноименные точки в каждом положении, получим годографы скоростей данных точек.

Модули скоростей точек в каждом положении можно получить умножением длины отрезка, соединяющего р и данную точку, на μ_υ.

                                                                                                 (15)

Например,

υ_в¹=рb1·μ_υ=100·0,0107=1,07(м/с)                                                               (16)

Планы скоростей для всех 12 положений можно увидеть на листе № 1.

Значения скоростей точек даны в таблице № 3.

Таблица 3 - Линейные скорости