Механика \ Техническая механика

Кинематика, динамика и конструирование привода поршневого компрессора, страница 12

Таблица 5 - Линейные ускорения точек звеньев

Положение

π-b’, мм

αB, м/с2

π-c’, мм

αC, м/с2

π-d’, мм

αD, м/с2

π-e’, мм

αE, м/с2

2

100

5,69

32

1,821

83

4,723

51

2,902

6

100

5,69

73,5

4,182

94

5,349

109,5

6,231

9

100

5,69

28

1,593

80

4,552

11

0,626

11

100

5,69

101

5,747

98,5

5,605

82

4,666

По свойствам планов ускорений можно найти угловые ускорения всех звеньев в данном положении по формуле:

εзв=                                                                                                          (38)

Для планов ускорений, изображенных на листе №1 с учетом масштабных коэффициентов формулы имеют вид:

ε2=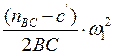                                                                                               (39)

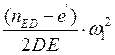ε4=                                                                                               (40)

Например,

ε22=(89/2·187,5) ·5,3382=6,763(1/с2).

В таблице 6 представлены угловые ускорения звеньев механизма во 2, 6, 9,11 положении.

Таблица 6 - Угловые ускорения звеньев

Положение

nCB-c’, мм

BC,  

мм

ε2,

с-2

nED-e’,     мм

ED,  

мм

ε4,      

с-2

2

89

187,5

6,763

70

200

4,986

6

27

187,5

2,052

15,5

200

1,104

9

100,5

187,5

7,636

81

200

5,770

11

45

187,5

3,419

37

200

2,636

Для определения направления углового ускорения звеньев, вектор тангенциального ускорения с планов ускорений переносим параллельно самому себе на план положений в точку, вокруг которой производится вращение.

Направление векторов угловых скоростей и угловых ускорений показаны на рисунке 8.

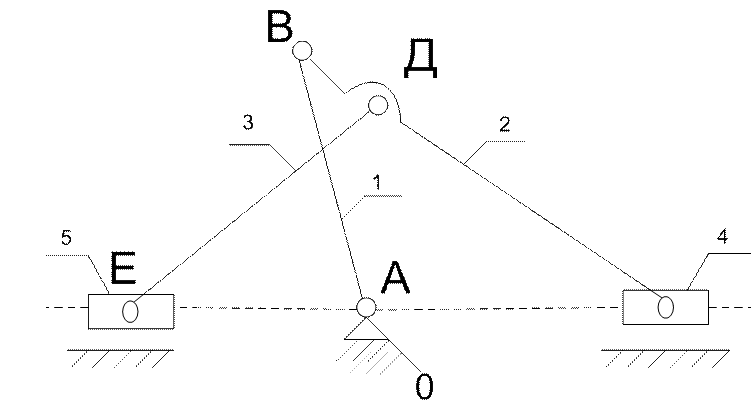
Рисунок 8 - Направления векторов угловых ускорений и угловых скоростей

1.6 Метод кинематических диаграмм

Метод кинематических диаграмм основан на представлении функции положения в виде графика S(φ), который получен на основе планов положений механизма. Первая и вторая передаточные функции получены также в виде графиков S’(φ) и S’’(φ) последовательным дифференцированием S(φ).

S(φ) - диаграмма перемещений;

S’(φ) - диаграмма аналогов скоростей;

S’’(φ)- диаграмма аналогов ускорений.

Достоинство метода - простота выполнения.

Недостатки: приближенный, позволяет получить только закон движения выходного звена механизма.

Строим диаграмму для точки Е5.

Все диаграммы строятся в одной системе координат. Диаграммы перемещений, аналогов скоростей и ускорений - масштабные графические изображения, поэтому для них выбирается определенный масштаб.  По оси абсцисс откладывают  угол поворота. Масштаб на этой оси

μφ=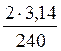=0,026(1/мм), где 240 - расстояние 0-12(положения).

На оси ординат откладывают расстояние Е0-Еί. Масштабный коэффициент этой оси μS=μS= μS=μl=0,004(м/мм).

1.6.1 Построение диаграмм перемещений.

Для построения диаграммы перемещений пользуются планом положений для точки Е.

Первая точка диаграммы перемещений будет находиться в начале системы, так как она строится для нулевого положения. Далее измеряют расстояние Е0-Е1 и отмечают его на перпендикуляре, проведенном из первого положения к оси абсцисс. Далее измеряют расстояние Е0-Еί и отмечают его на  ί-ом перпендикуляре. Соединив все полученные точки, получают диаграмму перемещений — S(φ).

Пример построения диаграмм перемещений показан на рисунке 9.

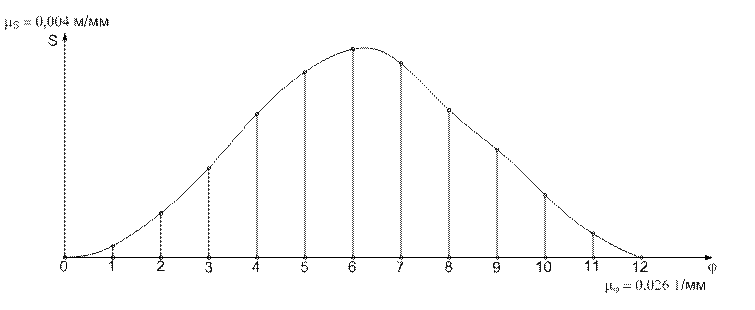
Рисунок 9 - Диаграмма перемещений

1.6.2 Построение диаграммы аналогов скоростей.

Для построения этой диаграммы нужно выбрать полюс Р по формуле:

ОР=240/6,28=38 (мм)                                                                                   (41)

Скачать файл