Кинематика, динамика и конструирование привода поршневого компрессора, страница 11

Для построения планов ускорений механизма поршневого компрессора   μ_α=(μ_l/2)·ω₁²                                                                                                 (22)

μ_α=(0,004/2) ·5,338²=0,0569(м/мм·с²).

Рассмотрим пример построения плана ускорений для второго положения.

На чертеже отмечаем полюс плана ускорений π.

Ускорение точки А равно нулю, следовательно она попадет в полюс.

Ускорение точки В определим из векторных уравнений:

α_В= α_А+α_В/А                                                                                                 (23)

α_В= α_В/Аⁿ+ α_В/А^τ                                                                                              (24)

Тангенциальное ускорение α_В/А^τ=0, так как угловое ускорение первого звена равно нулю. Поэтому точку b^’ на плане ускорений найдем как отрезок, проведенный через π, параллельно АВ с плана положений, направленного от В к А длиной 100 мм(2АВ).

Ускорение точки С определим также из векторных уравнений:

α_С= α_В+α_С/В                                                                                                (25)

α_С= α_С0+α_{С/ С0}                                                                                               (26)

α_С= α_В+ α_С/Вⁿ+ α_С/В^τ                                                                                       (27)

α_С= α _С0+ α_С/С0ⁿ+ α_{С/ С0}^τ                                                                                   (28)

Ускорение точки С₀=0, поэтому она попадет в полюс.

α_С/С0ⁿ=0,                                                                                                        (29)

точка движется по прямой, поэтому радиус кривизны равен бесконечности.

Тангенциальное ускорение α_С/С0^τ направлено параллельно горизонтали     х – х.

Расстояние от полюса до α_С/Вⁿ определяется по формуле:

b^’- α_С/Вⁿ= 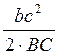==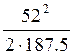7(мм)                                                                  (30)

Направлено это ускорение параллельно ВС с плана положений от С к В. Проводим этот отрезок через точку b^’ на плане ускорений.

Затем через конец вектора α_С/Вⁿ проводим вектор, перпендикулярный звену ВС с плана положений до пересечения с  х – х. Получаем ускорение α_С/В^τ. Соединив эту точку с точкой b^’ получим точку c^’. Вектор b^’c^’ - полное ускорение точки С.

Точку D на плане ускорений можно получить, используя теорему подобия:

b^’d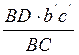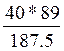^’===18.9(мм)                                                              (31)

Соединив π с d^’ получим ускорение точки D.

Ускорение точки Е строится аналогично точке С.

α_Е= α_D+α_E/D                                                                                                     (32)

α_E= α_E0+α_{E/ E0}                                                                                                   (33)

α_E= α_D+ α_E/Dⁿ+ α_E/D^τ                                                                                       (34)

α_E= α _E0+ α_E/E0ⁿ+ α_{E/ E0}^τ                                                                                    (35)

α _E0, α_E/E0ⁿ равны нулю, Е₀ принадлежит полюсу и ползун совершает поступательное движение.

d^’- α_Е/Dⁿ= 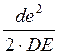==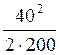4(мм)                                                                      (36)

Через точку d^’ проводим α_E/Dⁿ параллельно DE с плана положений, в направлении от Е к D длиной  4 мм. Через конец этого вектора проводим α_E/D^τ параллельно DE с плана положений до пересечения с горизонталью    х – х. Отмечаем точку e^’. Соединив d^’ с этой точкой получим полное ускорение точки Е.

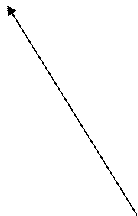
На рисунке 7 показан план ускорений для 2 положения.

                                                                            π, а

 

Рисунок 7 - Пример плана ускорений

Планы ускорений для 2,6,9, 11 положения даны на листе № 1.

Модули ускорений точек можно найти по формуле:

α_ί=( π-ί)·μ_α.                                                                                                   (37)

Для планов ускорений, построенных на листе № 1, рассчитываем ускорения по вышеприведенной формуле. Результаты расчета даны в таблице 5.   Например,

α_B²=100·0,0569=5,69(м/с).