Кинематика, динамика и конструирование привода поршневого компрессора, страница 19

Плечи сил определяются аналогично первой группе Ассура:                        l _R4-2=54·µ_l=0,214 (мм),

l _Pи2=81·µ _l=0,324 (мм),

l _G2=91·µ_l=0,364 (мм).

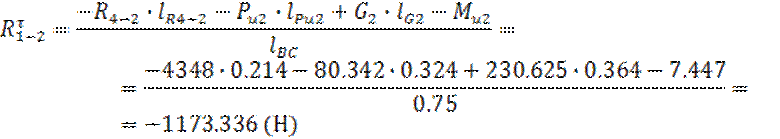Выражаем из этого уравнения R^τ_1-2:

Далее строим план сил для этой группы Ассура. Выбираем масштабный коэффициент µ_р2=20 (Н/мм)  и строим план сил, его пример изображен на рисунке 23.

     Rⁿ₁₂                                                  P_и5            G₂          

                                     R₄₂                                                                                           P_Σ3

                                                               R₃₂                                       G₃

     R^τ₁₂                                                                                                                                                                   

R₁₂                                                                                                   R₀₃

                                                                                                                                                                      

Рисунок 23 - План сил для группы Ассура (4-5)

Данный план сил аналогичен вышеописанному плану, только с учетом силы в паре D и направлению реакций согласно принципу равенства действия противодействию.

По этому плану мы нашли значения следующих сил умножением отрезка, показанному на плане на его масштабный коэффициент:

Rⁿ₁₂=425·20=8480 (H);

R₁₂=428·20=8560 (H);

R₀₃=38·20=760 (H).

Реакцию R₂₃ находим также из векторной суммы сил, действующих на данное звено:

P_Σ3+G₃+R₀₃+R₂₃=0                                                                                (68)

Так как данная сумма векторная, то реакцию R₂₃ мы также находим из плана сил: 

R₂₃=218·20=4360 (Н).

Далее выделяем начальный механизм, который представлен на рисунке 24, со всеми силами и реакциями, которые на него действуют.

                                             Р_ур                                            

                                                                               R₂₁

                                          1

                                          A             0

                                                            

R₀₁

Рисунок 24 - Начальный механизм

В данном случае мы не учитываем силу тяжести и силы инерции, так как кривошип является самым малым по размерам из всех звеньев.

Чтобы найти реакцию Р_ур, которая прикладывается перпендикулярно кривошипу составим уравнение моментов сил относительно точки А.

Р_ур·l_AB-R₂₁·l_R21=0                                                                                          (69)

Выражаем силу Р_ур:

Р_ур= (R₂₁·l_R21)/l_AB.                                                                                        (70)

Р_ур=(8560·0,182)/0,20=7789,6(Н).

Для вычисления реакции R₀₁ строим план сил, для которого выбираем масштабный коэффициент μ_р3=80 (Н/мм). План сил для начального механизма поршневого компрессора приведен на рисунке 25.

 

                              R₀₁       Р_ур

R₂₁

Рисунок 25 - План сил для начального механизма

2.10 Определение уравновешивающего момента на основе принципа возможных перемещений

Для равновесия механической системы необходимо и достаточно, чтобы сумма работ всех активных сил на любом возможном перемещении равнялась нулю.

К активным  силам относятся: силы полезных сопротивлений, веса звеньев механизма, инерционные нагрузки.

В случае, когда речь идет о механической системе, т.е. о механизме в целом, реакции в кинематических парах являются силами внутренними и не учитываются в принципе возможных перемещений, т.к. согласно третьему закону Ньютона эти реакции,  например R_ij=-R_ji, взаимно уничтожаются.

Аналитическое  выражение, описывающее принцип возможных перемещений составляется с учетом характера движения каждого подвижного звена механизма в пространстве и принимает вид:

ΣР_idS_icosL_i+ΣM_idφ_i=0,                                                                                  (71)